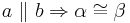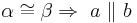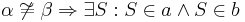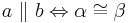Lösung von Aufgabe 5.2 (SoSe11): Unterschied zwischen den Versionen
Katrin (Diskussion | Beiträge) |
Katrin (Diskussion | Beiträge) |
||
| Zeile 24: | Zeile 24: | ||
Stimmt es,dass 4. dann keine äquivalente Aussage ist? Ist das so, weil der Stufenwinkelsatz nur ein Satz ist, und keine Äquivalenz? "[[Benutzer:Michi6889|Michi6889]] 17:34, 14. Mai 2011 (CEST)" | Stimmt es,dass 4. dann keine äquivalente Aussage ist? Ist das so, weil der Stufenwinkelsatz nur ein Satz ist, und keine Äquivalenz? "[[Benutzer:Michi6889|Michi6889]] 17:34, 14. Mai 2011 (CEST)" | ||
| − | Stimmt, denn das Kriterium beinhaltet neben dem Satz auch die Umkehrung und nach Adam Riese ist 2 > 1 (Im Kriterium hast du zwei hinreichende und notwendige Bedingungen, im Satz bzw. der Umkehrung je nur eine) --[[Benutzer:HecklF|Flo60]] 20:39, 14. Mai 2011 (CEST) | + | Stimmt, denn das Kriterium beinhaltet neben dem Satz auch die Umkehrung und nach Adam Riese ist 2 > 1 (Im Kriterium hast du zwei hinreichende und notwendige Bedingungen, im Satz bzw. der Umkehrung je nur eine) --[[Benutzer:HecklF|Flo60]] 20:39, 14. Mai 2011 (CEST)<br> |
3. ist die Kontraposition zum Stufenwinkelsatz und somit eine äquivalente Aussage.--[[Benutzer:Katrin|Katrin]] 17:39, 18. Jun. 2011 (CEST) | 3. ist die Kontraposition zum Stufenwinkelsatz und somit eine äquivalente Aussage.--[[Benutzer:Katrin|Katrin]] 17:39, 18. Jun. 2011 (CEST) | ||
Version vom 18. Juni 2011, 16:40 Uhr
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt S geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel 
und 
. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
a) Es seien a und b zwei nichtidentische Geraden, die von einer dritten Geraden geschnitten werden. Dabei entstehen die Winkel und . Diese Winkel sind kongruent zueinander, wenn die Geraden a und b parallel zueinander sind.
a und b müssen parallel sein, somit ist deine Def. falsch!Mathegott 18:45, 7. Jun. 2011 (CEST)
b) Version 1 und 2 können als "genau dann wenn" Aussage zusammengefasst werden
beI 3. fehlt, dass in diesem Fall die Geraden nicht parallel sein dürfen
4. stellt die Kombination aus 1 und 2 dar--Flo 21 14:33, 5. Mai 2011 (CEST)
Bei welcher Aussage handelt es sich denn um den Stufelwinkelsatz? Ist eine der Aussagen eine Umkehrung des Stufenwinkelsatzes?--Tutor Andreas 13:20, 6. Mai 2011 (CEST) Liest man die Aufgabe, dann werden auch die Antworten klar!--Flo 21 19:47, 8. Mai 2011 (CEST)
a) Stufenwinkelsatz: Stufenwinkel an zwei geschnittenen Parallelen sind kongruent zueinander.--Engel81 18:36, 6. Mai 2011 (CEST)
b) 1. ist der Stufenwinkelsatz, 2. die Umkehrung und 4. die Zusammenfassung--Matthias 19:01, 8. Mai 2011 (CEST)
Man könnte, wie hier schon beschrieben wurde, 4. als eine "Zusammenfassung" von 1. und 2. beschreiben, also eine Art "Stufenwinkelkriterium". Um was handelt es sich beim 3. Punkt? Flo21 hat weiter oben schon etwas dazu gesagt und vllt. könnte man an dieser Stelle noch einmal darüber diskutieren.--Tutor Andreas 12:56, 13. Mai 2011 (CEST)
Der 3. Punkt ist die Kontraposition.--Matthias 10:39, 14. Mai 2011 (CEST)
ja, richtig. Ist 3. dann eine äuquivalente Aussage zum Stufenwinkelsatz?--Schnirch 14:13, 9. Jun. 2011 (CEST)
Stimmt es,dass 4. dann keine äquivalente Aussage ist? Ist das so, weil der Stufenwinkelsatz nur ein Satz ist, und keine Äquivalenz? "Michi6889 17:34, 14. Mai 2011 (CEST)"
Stimmt, denn das Kriterium beinhaltet neben dem Satz auch die Umkehrung und nach Adam Riese ist 2 > 1 (Im Kriterium hast du zwei hinreichende und notwendige Bedingungen, im Satz bzw. der Umkehrung je nur eine) --Flo60 20:39, 14. Mai 2011 (CEST)
3. ist die Kontraposition zum Stufenwinkelsatz und somit eine äquivalente Aussage.--Katrin 17:39, 18. Jun. 2011 (CEST)
