Basiswinkelsatz und Mittelsenkrechtenkriterium (SoSe 11): Unterschied zwischen den Versionen
(→Satz VII.6 b (notwendige Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von \overline{AB} gehört)) |
HecklF (Diskussion | Beiträge) (→Ein im Rahmen unserer Theorie korrekter Beweis des Basiswinkelsatzes) |
||
| Zeile 65: | Zeile 65: | ||
===== Ein im Rahmen unserer Theorie korrekter Beweis des Basiswinkelsatzes ===== | ===== Ein im Rahmen unserer Theorie korrekter Beweis des Basiswinkelsatzes ===== | ||
Probieren Sie ruhig weitere Varianten: Mittelsenkrechte ... . | Probieren Sie ruhig weitere Varianten: Mittelsenkrechte ... . | ||
| − | Letztlich hilft nur die Winkelhalbierende. Damit wir uns auf die wesentliche Beweisidee des Basiwinkelsatzes konzentrieren können, schicken wir ein Lemma voraus. | + | Letztlich hilft nur die Winkelhalbierende. Damit wir uns auf die wesentliche Beweisidee des Basiwinkelsatzes konzentrieren können, schicken wir ein Lemma voraus.<br /><br /> |
| + | Das finde ich ganz schön gemein von den Dozenten ein unschuldiges Lemma vorauszuschicken. Es ist doch noch so klein. Naja, um sauber beweisen zu können müssen wir dieses Opfer wohl bringen. Dann mach es gut kleines Lemma, pass gut auf dich auf und vielleicht sehen wir uns ja irgendwann wieder :-) --[[Benutzer:HecklF|Flo60]] 21:14, 7. Jul. 2011 (CEST) | ||
======Lemma 1====== | ======Lemma 1====== | ||
::Die Winkelhalbierende <math>\ SW^+</math> eines Winkels <math>\ \angle ASB</math> schneidet die Strecke <math>\overline{AB}</math> in genau einem Punkt <math>\ P</math>. | ::Die Winkelhalbierende <math>\ SW^+</math> eines Winkels <math>\ \angle ASB</math> schneidet die Strecke <math>\overline{AB}</math> in genau einem Punkt <math>\ P</math>. | ||
Version vom 7. Juli 2011, 20:14 Uhr
Inhaltsverzeichnis |
Der Basiswinkelsatz
Gleichschenklige Dreiecke
Definition VII.4 : (gleichschenkliges Dreieck)
Das können sie selbst. Bringen Sie in der Definition die Begriffe Basis, Basiswinkel und Schenkel eines gleichschenkligen Dreiecks unter.
Übungsaufgabe
Der Basiswinkelsatz
Satz VII.5: Basiswinkelsatz
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Der folgende Beweis ist für die Schule ok. hier jedoch nicht zugelassen
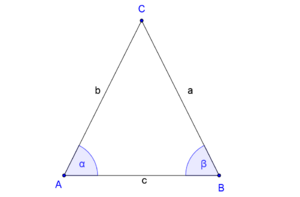
Es sei  ein Dreieck mit den schulüblichen Bezeichnungen. o.B.d.A. seien die Seiten
ein Dreieck mit den schulüblichen Bezeichnungen. o.B.d.A. seien die Seiten  und
und  kongruent zueinander:
kongruent zueinander:
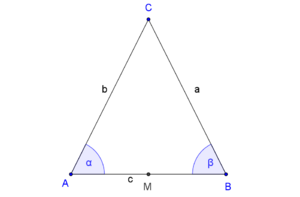
Nach der Existenz und Eindeutigkeit des Mittelpunktes einer Strecke existiert der Mittelpunkt  der Dreiecksseite
der Dreiecksseite  .
.
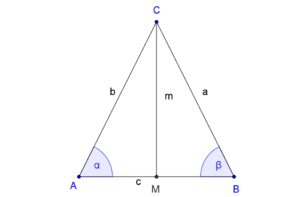
Wir werden jetzt zeigen, dass die beiden Teildreiecke 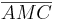 und
und 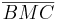 kongruent zueinander sind:
kongruent zueinander sind:
Nachweis von 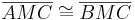 :
:
| Nr. | Skizze | Beweisschritt | Begründung |
|---|---|---|---|
| (1) | 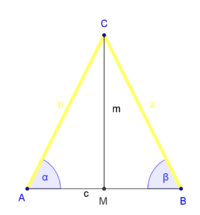
|
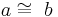
|
Voraussetzung |
| (2) | 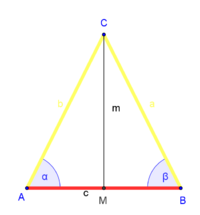
|
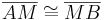
|
 ist Mittelpunkt von ist Mittelpunkt von 
|
| (3) | 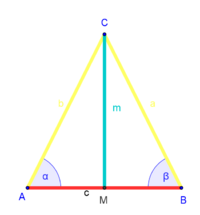
|
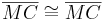
|
trivial (oder Reflexivität der Kongruenzrelation) |
| (4) | 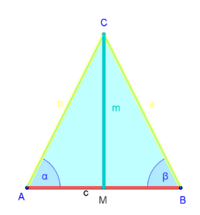
|
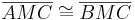
|
(1), (2), (3), SSS |
Wegen (4) gilt nun auch 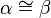 .
.
w.z.b.w.
Ein schöner einfacher Beweis, leider hat er hier keine Gültigkeit. Warum?
Da wir für den Beweis vom SSS den Basiswinkelsatz benutzen, deswegen dürfen wir nicht für den Beweis vom Basiswinkelsatz den SSS benutzen. --Peterpummel 20:41, 1. Jul. 2011 (CEST)
Ein im Rahmen unserer Theorie korrekter Beweis des Basiswinkelsatzes
Probieren Sie ruhig weitere Varianten: Mittelsenkrechte ... .
Letztlich hilft nur die Winkelhalbierende. Damit wir uns auf die wesentliche Beweisidee des Basiwinkelsatzes konzentrieren können, schicken wir ein Lemma voraus.
Das finde ich ganz schön gemein von den Dozenten ein unschuldiges Lemma vorauszuschicken. Es ist doch noch so klein. Naja, um sauber beweisen zu können müssen wir dieses Opfer wohl bringen. Dann mach es gut kleines Lemma, pass gut auf dich auf und vielleicht sehen wir uns ja irgendwann wieder :-) --Flo60 21:14, 7. Jul. 2011 (CEST)
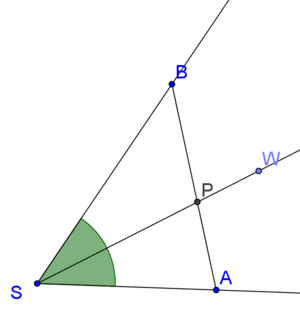
Lemma 1
- Die Winkelhalbierende
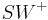 eines Winkels
eines Winkels  schneidet die Strecke
schneidet die Strecke  in genau einem Punkt
in genau einem Punkt  .
.
- Die Winkelhalbierende
Beweis von Lemma 1
später (Wir haben wichtigeres zu tun.) googeln Sie: "Geschichten aus dem Inneren Gieding" und Sie werden fündig.
Beweis des Basiswinkelsatzes
Das Mittelsenkrechtenkriterium
Satz VII.6: (Mittelsenkrechtenkriterium)
- Eine Menge
 von Punkten ist genau dann die Mittelsenkrechte einer Strecke
von Punkten ist genau dann die Mittelsenkrechte einer Strecke  , wenn für jeden Punkt
, wenn für jeden Punkt 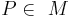 gilt:
gilt: 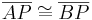 .
.
- Eine Menge
Anmerkung:
Dann wäre doch auch der Mittelpunkt, als Menge aufgefasst, einer Strecke unsere Mittelsenkrechte der Strecke, macht das Sinn ?
Dann gäbe es ja mehrer Mittelsenkrechten einer Strecke und das ist ein Widerspruch zu unserer Definition, bzw. zu der Eindeutigkeit. Warum steht bei dem Kriterium nicht einfach Grade anstelle von "Menge von Punkte "
--Peterpummel 20:46, 1. Jul. 2011 (CEST)
Peterpummel, Sie haben vollkommen recht - super. Wie müsste das Kriterium demnach korrekt lauten?--Schnirch 13:20, 4. Jul. 2011 (CEST)
Bezug zur Schule:
Konstruktion der Mittelsenkrechten einer Strecke  mittels Zirkel und Lineal:
mittels Zirkel und Lineal:
Konstruktionsvorschrift:
gegeben: Strecke 
gesucht:  , die Mittelsenkrechte von
, die Mittelsenkrechte von 
| Schrittnr. | Konstruktionsschritt |
|---|---|
| 1. | Zeichne einen Kreis um  , dessen Radius , dessen Radius 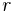 länger als die Hälfte der Länge der Strecke länger als die Hälfte der Länge der Strecke  ist. ist.
|
| 2. | Behalte 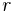 bei und zeichne einen Kreis um bei und zeichne einen Kreis um  . .
|
| 3. | Der Kreis um  schneidet den Kreis um schneidet den Kreis um  in den beiden Schnittpunkten in den beiden Schnittpunkten 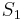 und und 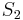 . .
|
| 4. | Zeichne die Gerade 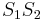 . Sie ist die gesuchte Mittelsenkrechte von . Sie ist die gesuchte Mittelsenkrechte von  . .
|
Frage: Ist dieser Algorithmus korrekt? Anders gefragt: Ist 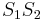 wirklich die Mittelsenkrechte von
wirklich die Mittelsenkrechte von  ?
?
Wir beweisen die Korrektheit der Konstruktion indem wir folgendes zeigen:
Satz VII.6 a: (hinreichende Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von  gehört.)
gehört.)
- Wenn ein Punkt
 zu den Endpunkten der Strecke
zu den Endpunkten der Strecke  jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von
jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von  .
.
- Wenn ein Punkt
Beweis von Satz VII.6 a
Übungsaufgabe (Das Video hilft)
Nach dem Beweis von Satz VII.6 a wissen wir, dass die beiden Punkte 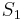 und
und 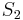 Punkte der Mittelsenkrechten von
Punkte der Mittelsenkrechten von  sind.
sind.
Die Wahl des Radius 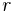 der beiden Kreise in unserer Konstruktion war beliebig für
der beiden Kreise in unserer Konstruktion war beliebig für 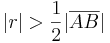 . Wir stellen uns jetzt die frage, ob wir jeden beliebigen Punkt unserer Mittelsenkrechten als Schnittpunkt zweier entsprechender Kreise konstruieren könnten.
. Wir stellen uns jetzt die frage, ob wir jeden beliebigen Punkt unserer Mittelsenkrechten als Schnittpunkt zweier entsprechender Kreise konstruieren könnten.
Die Frage anders formuliert:
Hat jeder Punkt der Mittelsenkrechten von  zu den Punkten
zu den Punkten  und
und  jeweils ein und denselben Abstand?
jeweils ein und denselben Abstand?
Noch anders formuliert:
Hat jeder Punkt der Mittelsenkrechten einer Strecke  notwendigerweise zu
notwendigerweise zu  und zu
und zu  ein und denselben Abstand?
ein und denselben Abstand?
Der folgende Satz VII.6 b beantwortet diese beiden Fragen postiv:
Satz VII.6 b (notwendige Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von  gehört)
gehört)
- Wenn ein Punkt
 zur Mittelsenkrechten der Strecke
zur Mittelsenkrechten der Strecke  gehört, dann hat er zu den Punkten
gehört, dann hat er zu den Punkten  und
und  ein und denselben Abstand.
ein und denselben Abstand.
- Wenn ein Punkt
Beweis: Übungsaufgabe