Diskussion:Basiswinkelsatz und Mittelsenkrechtenkriterium (SoSe 11)
Inhaltsverzeichnis |
Diskussion zu Satz VI.6
Satz VII.6: (Mittelsenkrechtenkriterium)
- Eine Menge
 von Punkten ist genau dann die Mittelsenkrechte einer Strecke
von Punkten ist genau dann die Mittelsenkrechte einer Strecke  , wenn für jeden Punkt
, wenn für jeden Punkt 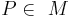 gilt:
gilt: 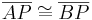 .
.
- Eine Menge
Anmerkung:
Bemerkungen von Peterpummel
Dann wäre doch auch der Mittelpunkt, als Menge aufgefasst, einer Strecke unsere Mittelsenkrechte der Strecke, macht das Sinn ?
Dann gäbe es ja mehrer Mittelsenkrechten einer Strecke und das ist ein Widerspruch zu unserer Definition, bzw. zu der Eindeutigkeit. Warum steht bei dem Kriterium nicht einfach Grade anstelle von "Menge von Punkte "
--Peterpummel 20:46, 1. Jul. 2011 (CEST)
Bemerkung vom Kollegen Schnirch
Peterpummel, Sie haben vollkommen recht - super. Wie müsste das Kriterium demnach korrekt lauten?--Schnirch 13:20, 4. Jul. 2011 (CEST)
m.g.
So wie Satz VI.6 formuliert wurde, ist er wirklich nicht korrekt. Korrekt müsste es heißen:
- Eine Menge
 von Punkten ist genau dann die Mittelsenkrechte einer Strecke
von Punkten ist genau dann die Mittelsenkrechte einer Strecke  , wenn sie die Menge aller Punkte
, wenn sie die Menge aller Punkte  mit
mit 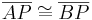 ist.
ist.
- Eine Menge
Die Verwirrung kam wie folgt zustande:
Ein Kriterium ist geeignet, eine weitere neue Definition eines Begriffs zu formulieren. Um das zu verdeutlichen, wollte ich mit der Formulierung des Kriteriums gleichzeitig auf die Definition des Begriffs Mittelsenkrechte als Menge aller Punkte, die zu den Endpunkten einer Strecke ein und denselben Abstand haben, hinaus. Korrekt wird dieses Unterfangen nur gelingen, wenn das Kriterium quasi von der Formulierung her gleichzeitig als Definition dienen kann. Trotzdem wollte ich aus irgendwelchen pseudodidaktischen Ideen heraus , dass sich Kriterium und Definition sprachlich stärker unterscheiden. Im Endeffekt ist dann alles falsch geworden.
Wenn ich den Begriff der Geraden im Kriterium verwende, brauche ich nur zwei Punkte anzusprechen:
- Eine Gerade
 ist genau dann Mittelsenkrechte der Strecke
ist genau dann Mittelsenkrechte der Strecke  , wenn
, wenn  zwei Punkte enthält, die zu
zwei Punkte enthält, die zu  und zu
und zu  jedweils ein und denselben Abstand haben.
jedweils ein und denselben Abstand haben.
- Eine Gerade
Jetzt kann ich beweisen, dass jeder Punkt von  zu den Punkten
zu den Punkten  und
und  jeweils ein und denselben Abstand hat.
jeweils ein und denselben Abstand hat.
Mein Dilemma war also das Folgende: Verwende ich den Begriff der Geraden, brauche ich nur zwei Punkte. Verwende ich alle Punkte brauche ich nicht Gerade zu verwenden, weil sich beweisen lässt, dass die Menge aller Punkte die zu  und
und  jeweils ein und denselben Abstand haben, eine Gerade bilden.
jeweils ein und denselben Abstand haben, eine Gerade bilden.
Hinsichtlich eines Satzes ist das alles nicht so problematisch, wenn man jedoch so wie ich es wollte, mit dem Kriterium gleichzeitig sprachlich die neue Definition entstehen lassen will, wird es zu einem Problem.
Ich formuliere das Kriterium neu:
- Ein Punkt
 ist genau dann ein Punkt der Mittelsenkrechten der Strecke
ist genau dann ein Punkt der Mittelsenkrechten der Strecke  , wenn
, wenn 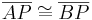 gilt.
gilt.
- Ein Punkt
--*m.g.* 19:18, 9. Jul. 2011 (CEST)

