Tangentenkriterium: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
HecklF (Diskussion | Beiträge) (→Satz 1: (Tangete am Kreis)) |
HecklF (Diskussion | Beiträge) (→Satz 1: (Tangete am Kreis)) |
||
| Zeile 25: | Zeile 25: | ||
| 5 || Somit ist nach der Dreieckskongruenz und aus (4) |MC| = |MA| = r nach Voraussetzung und es ergeben sich zwei Schnittpunkte, was ein Widerspruch zur Voraussetzung ist. | | 5 || Somit ist nach der Dreieckskongruenz und aus (4) |MC| = |MA| = r nach Voraussetzung und es ergeben sich zwei Schnittpunkte, was ein Widerspruch zur Voraussetzung ist. | ||
|} | |} | ||
| + | <br /> | ||
| + | <ggb_applet width="1366" height="604" version="3.2" ggbBase64="UEsDBBQACAAIADJV+D4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VhNc+I4ED3v/AqV7zi2/EkVZMphL6lKNluVmTnsTdgCtNiWV5ITyK/flmSDgYRNNkntBxfjVtNqvfe6W8nk66Yq0QMVkvF66viu5yBa57xg9XLqtGoxSp2vl18mS8qXdC4IWnBRETV1Ahc72t6yyy8/TeSKPyJSGpcfjD5OnQUpJXWQbAQlhVxRqg7spN2wkhGxvZv/TnMl9ws2yHXdtLCLEi3Y8qq4YbJ/vTAbNiVTP7MHVlCBSp5PnTiC1OHbDyoUy0k5dULPWvDUwUeLYAr06ooL9sRrpd33wUsypyUAcK+2JUXoQa8GdmkBzghJ9kQBLKxtkwuDwYS2eckKRmp9TpMiOCH0yAq1At8gjmE7ypYrOEfsYRsu51wU91upaIU2v1HBIVU/0iRs7Vtg3yTkDDtGnlkavpkw9OGeKgUZS0Q2dA/mUrDi4OVaXvFyb2o4q9WMNKoVhu+gM5mDTx3YS+iEs3pZ0s6GgY4Vzddzvrm3KAQ29LdtY35iEpovZ7zkAgkNfQQO3XNun8ZHZ7rz8oyPZzy6GDrobt0fY+NhnnP7tFyx2qbWndzvT+17/TZMIm3QMIJMd4c3LE8dB7U1Uzf9C8hj3R3Vtz/4pa3mUB9Dgexi+h8Vc3JxpJ/JmoqallYkNXDb8lZaKdq9TCIFzVkFr3ahg4Rour5DAtZa0KWgfeK2uixgZtUbCvHIPLnok9A5SMg1V9Am4DxKn0VXsYIK0t8KorRF10FJKwpFoowejJx2uNw6u2bBTd33Fd6t7xGG5We1YVREymZFwNLLvyRb6ALD45h4t7w4PCSpASxzAii4RgfQdDSUFl3nU52GUQMhTUUMsDYQSbTR0nJj7A0+EGarQ0Qgzicby/zEFpPuA/seAkxbhP4Cq6v/B1apm6QGnRFEiN8GT86ritQFqkkFW82YyEtqUGF6OiDiaUUh4muwLBKt6hfWNlgX4gRr0DPLd1iuncNWolZQsTWV0vQ7Nexs7yHEezUdd4uFpErjNwqtuEY4OkfXq3KH6UPrB8icC4nQxuuY3Ho2IfTUWza+4Uuv+Z3pyR8QB8oQbIOy3j/rvTKsqyN10zROh9WRBd0WWQiRn6ufLNILuoJsqn/U9jjS9k1QXs4WQNlZidzTpba/ViPkvEZkF60nmHyESgZF8n6ZnMhg0KPcuKs7303DA7BtFY70zSIMk/H+8xYpHfHDKriQ5UztMC51T7iuFUw5aqbG6fBaU9roW8Nd/U2QWuqbpfUZDMUXiL4TMHiWvCblDWR7xPeV5Zuc8K3O860Pvq/mf29LCDxDbBK+Vgmn/G97gXRCgHrd+/jhBwnhZf5+NaPukDZ1wld2nq/DeZn9rXnpY3s7Nc9PnZmvnphjFyeJl2A/DsdhGuo7hR2fCZSrj4PE94PQw174nmH6TNl0bTI7oSF/Q9nk/6UeiV2MDyCN+o4ZhHiMkzSIvMiPwrG91o0wzKcUBte4Z+fzC+WWCcHFEVPZSwNt9paCmf3zBTO8JuJ0CHlimPDcID3U/LtEf/Z6MDtBs3jb9aD4ROn3f0T7UWBQj/yPuSP4QRSlSYyh/0fjZBx3V003CIYdyII+St3IS6Kx19P0Uer/lPvCxfAvVvNfmu4/WJd/AlBLBwgQuyqXwwQAAPMSAABQSwECFAAUAAgACAAyVfg+ELsql8MEAADzEgAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAP0EAAAAAA==" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
<br /> | <br /> | ||
--[[Benutzer:HecklF|Flo60]] 10:53, 24. Jul. 2011 (CEST) | --[[Benutzer:HecklF|Flo60]] 10:53, 24. Jul. 2011 (CEST) | ||
Version vom 24. Juli 2011, 10:00 Uhr
Inhaltsverzeichnis |
Tangentenkriterium
Kriterium: (Tangete am Kreis)
- Eine Gerade t, die durch einen Punkt A eines Kreises k mit dem Mittelpunkt M verläuft, ist genau dann Tangente an k, wenn t senkrecht auf MA steht.
- Eine Gerade t, die durch einen Punkt A eines Kreises k mit dem Mittelpunkt M verläuft, ist genau dann Tangente an k, wenn t senkrecht auf MA steht.
Satz 1: (Tangete am Kreis)
Beweis durch Wiederspruch:
Voraussetzung: 
Behauptung: 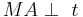
Annahme: 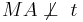
| 1 | Es existiert ein Lot von M auf t, dieses ist eindeutig. Der Lotfußpunkt auf k heiße B. | Ex. und Eindeutigkeit Lot, Annahme, Voraussetzung |
| 2 | CB| = |BA| | Axiom vom Lineal, Abstandsaxiom, Definition zwischenrelation, Voraussetzung, (1) und Skizze |
| 3 | 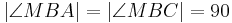 |
nach Konstruktion, Def. NW, Def. supplementär, Supplementaxiom, Def. Lot (1) |
| 4 | 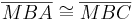 |
SWS, (2), (3) und weil trivialerweise  zu sich selbst kongruent ist. zu sich selbst kongruent ist.
|
| 5 | MC| = |MA| = r nach Voraussetzung und es ergeben sich zwei Schnittpunkte, was ein Widerspruch zur Voraussetzung ist. |
--Flo60 10:53, 24. Jul. 2011 (CEST)
Satz 2: (Tangente am Kreis)
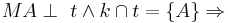 t ist Tangente an k.
t ist Tangente an k.
Eigentlich erscheint dieser Beweis komisch. Allerdings könnte es ja sein, dass wenn eine Gerade durch eben einen Punkt A verläuft und senkrecht auf dem Berührradius steht, dass dann trotzdem ein zweiter Schnittpunkt vorhanden ist mit k und dann wäre halt t keine Tangente mehr.
Voraussetzung: 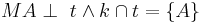
Behauptung: t ist Tangente an k
Annahme: Es ex. ein Punkt S: 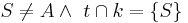
Ich versuche diesen Beweis bewusst in der absoluten Geometrie zu Beweisen. Mit der Innenwinklesumme wäre es natürlich noch einfacher, aber zwecks der Übung.
| 1 |  |
Annahme, Definiton Kreis und Radius |
| 2 | 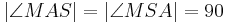 |
Voraussetzung, Basiswinkelsatz, (1), Def. Senkrecht |
| 3 | Demnach sind im Dreieck zwei Winkel nicht spitz, was ein Widerspruch zu einem der Korollare ist. Demnach ist die Annahme zu verwerfen. | Korollar des schwachen Außenwinkelsatzes, (2), Definition Dreieck |
--Flo60 10:53, 24. Jul. 2011 (CEST)