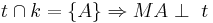Tangentenkriterium
Inhaltsverzeichnis |
Tangentenkriterium
Kriterium: (Tangete am Kreis)
- Eine Gerade t, die durch einen Punkt A eines Kreises k mit dem Mittelpunkt M verläuft, ist genau dann Tangente an k, wenn t senkrecht auf MA steht.
- Eine Gerade t, die durch einen Punkt A eines Kreises k mit dem Mittelpunkt M verläuft, ist genau dann Tangente an k, wenn t senkrecht auf MA steht.
Satz 1: (Tangete am Kreis)
Beweis durch Wiederspruch:
Voraussetzung: 
Behauptung: 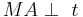
Annahme: 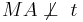
| 1 | Es existiert ein Lot von M auf t, dieses ist eindeutig. Der Lotfußpunkt auf k heiße B. | Ex. und Eindeutigkeit Lot, Annahme, Voraussetzung |
| 2 | Es existiert genau ein Punkt C für den gilt, dass o. B. d. A. 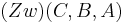 und und  |
Axiom vom Lineal, Abstandsaxiom, Definition zwischenrelation, Voraussetzung, (1) und Skizze |
| 3 | 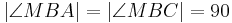 |
nach Konstruktion, Def. NW, Def. supplementär, Supplementaxiom, Def. Lot (1) |
| 4 | 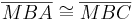 |
SWS, (2), (3) und weil trivialerweise  zu sich selbst kongruent ist. zu sich selbst kongruent ist.
|
| 5 | Somit ist nach der Dreieckskongruenz und aus (4) 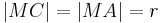 nach Voraussetzung und es ergeben sich zwei Schnittpunkte, was ein Widerspruch zur Voraussetzung ist. nach Voraussetzung und es ergeben sich zwei Schnittpunkte, was ein Widerspruch zur Voraussetzung ist.
|
--Flo60 10:53, 24. Jul. 2011 (CEST)
Beweisidee und Begründung ist richtig. Schöner wäre der Beweis sicher, wenn du mehrer kleinen Schritte aufführst, anstatt mit 6 Begründungen einen riesen Schritt durchführst.--Tutorin Anne 16:31, 24. Jul. 2011 (CEST)
Danke für den Hinweis, das Wiki streicht viele Aspekte heraus, wenn man mit "|" in der Tabelle arbeitet - ich habs geändert. --Flo60 19:14, 24. Jul. 2011 (CEST)
Satz 2: (Tangente am Kreis)
 t schneidet k im Punkt A
t schneidet k im Punkt A  t ist Tangente an k.
t ist Tangente an k.
Eigentlich erscheint dieser Beweis komisch. Allerdings könnte es ja sein, dass wenn eine Gerade durch eben einen Punkt A verläuft und senkrecht auf dem Berührradius steht, dass dann trotzdem ein zweiter Schnittpunkt vorhanden ist mit k und dann wäre halt t keine Tangente mehr.
Einschub von --WikiNutzer 13:21, 26. Jul. 2011 (CEST): Wenn in der Voraussetzung steht: ::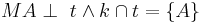 , heißt das dann nicht schon, dass es nur einen Schnittpunkt von t und k gibt? Vermutlich ist aber genau das zu beweisen, denn dass eine Gerade, die einen Kreis in genau einem Punkt schneidet, Tangente heißt, ist doch Definition und nicht Satz. Vielleicht wäre ::
, heißt das dann nicht schon, dass es nur einen Schnittpunkt von t und k gibt? Vermutlich ist aber genau das zu beweisen, denn dass eine Gerade, die einen Kreis in genau einem Punkt schneidet, Tangente heißt, ist doch Definition und nicht Satz. Vielleicht wäre ::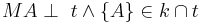 besser in der Voraussetzung? [Einschub von --WikiNutzer 13:21, 26. Jul. 2011 (CEST) Ende]
besser in der Voraussetzung? [Einschub von --WikiNutzer 13:21, 26. Jul. 2011 (CEST) Ende]
Da hast du aus meiner Sicht vollkommen recht. Ich habe es abgeändert (in Worten, deines wäre denke ich genauso richtig gewesen). --Flo60 21:42, 27. Jul. 2011 (CEST)
Voraussetzung: 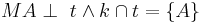
Behauptung: t ist Tangente an k
Annahme: Es ex. ein Punkt S: 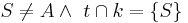
Ich versuche diesen Beweis bewusst in der absoluten Geometrie zu Beweisen. Mit der Innenwinklesumme wäre es natürlich noch einfacher, aber zwecks der Übung.
| 1 |  |
Annahme, Definiton Kreis und Radius |
| 2 | 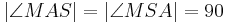 |
Voraussetzung, Basiswinkelsatz, (1), Def. Senkrecht |
| 3 | Demnach sind im Dreieck zwei Winkel nicht spitz, was ein Widerspruch zu einem der Korollare ist. Demnach ist die Annahme zu verwerfen. | Korollar des schwachen Außenwinkelsatzes, (2), Definition Dreieck |
--Flo60 10:53, 24. Jul. 2011 (CEST)
Gut! Aber auch hier lieber ein paar Schritte mehr!--Tutorin Anne 16:34, 24. Jul. 2011 (CEST)
Wieso wird bei der Umkehrung eine Senkrechte auf dem Radius ausgeschlossen? Die Umkehrung lautet doch: Wenn t senkrecht auf MA, dann ist t Tangente. Und t kann doch Senkrecht auf MA stehen und den Kreis zweimal schneiden?
--Verteidigungswolf 17:44, 26. Jul. 2011 (CEST) Du hast recht, die Voraussetzung ist nicht richtig. Es darf nicht angegeben werden, dass Kreis und Gerade genau einen Schnittpunkt A haben. --Tutorin Anne 18:38, 28. Jul. 2011 (CEST)