Serie 05: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 5.1) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 5.2) |
||
| Zeile 11: | Zeile 11: | ||
=Aufgabe 5.2= | =Aufgabe 5.2= | ||
| − | Das Bild aus Aufgabe 5.1 suggeriert, dass die Mittelsenkrechten von <math>\overline{B'_1B'}</math> und <math>\overline{A'_1A'}</math> identisch sind. Zeigen Sie, dass es Fälle gibt, in denen dieselben Voraussetzungen wie in Aufgabe 5.1 gelten, die genannten beiden Mittelsenkrechten jedoch nicht identisch sind. | + | Das Bild aus Aufgabe 5.1 suggeriert, dass die Mittelsenkrechten von <math>\overline{B'_1B'}</math> und <math>\overline{A'_1A'}</math> identisch sind. Zeigen Sie mittels einer Skizze, dass es Fälle gibt, in denen dieselben Voraussetzungen wie in Aufgabe 5.1 gelten, die genannten beiden Mittelsenkrechten jedoch nicht identisch sind. |
| + | =Aufgabe 5.3= | ||
Version vom 22. November 2011, 13:40 Uhr
Aufgabe 5.1
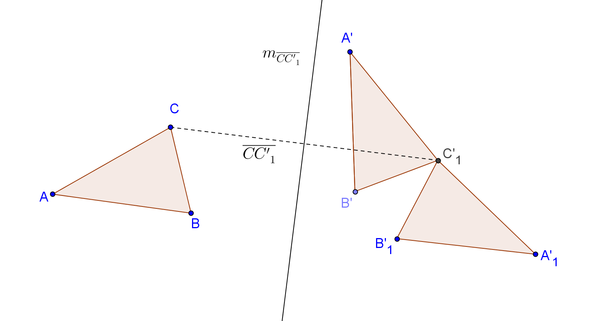
Es sei Fehler beim Parsen(Syntaxfehler): \overline{A'B'C'_1
das Bild vonbei einer Bewegung
.
Fehler beim Parsen(Syntaxfehler): \overline{A'_1B'_1C'_1
sei das Bild von.
Beweisen Sie:
Die Mittelsenkrechte von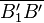 
geht durch den Punkt 
.
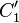Die Mittelsenkrechte von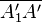 
geht durch den Punkt .
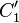Aufgabe 5.2
Das Bild aus Aufgabe 5.1 suggeriert, dass die Mittelsenkrechten von 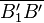und 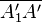identisch sind. Zeigen Sie mittels einer Skizze, dass es Fälle gibt, in denen dieselben Voraussetzungen wie in Aufgabe 5.1 gelten, die genannten beiden Mittelsenkrechten jedoch nicht identisch sind.
