Lösung von Aufg. 7.7 (WS 11/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
RicRic (Diskussion | Beiträge) |
|||
| Zeile 6: | Zeile 6: | ||
Es seien A und B zwei verschiedene Punkte. Die Halbgerade <math>\ AB^{-} </math> ist die Punktmenge aller Punkte P, für die gilt: | Es seien A und B zwei verschiedene Punkte. Die Halbgerade <math>\ AB^{-} </math> ist die Punktmenge aller Punkte P, für die gilt: | ||
<math>\forall </math> P : <math>\operatorname(Zw) (P, A, B) </math> vereinigt mit {A} --[[Benutzer:Teufelchen777|Teufelchen777]] 01:10, 25. Nov. 2011 (CET) | <math>\forall </math> P : <math>\operatorname(Zw) (P, A, B) </math> vereinigt mit {A} --[[Benutzer:Teufelchen777|Teufelchen777]] 01:10, 25. Nov. 2011 (CET) | ||
| + | <br /><br /> | ||
| + | Vorausgesetzt die Definition aus Aufg. 7.6<br /> | ||
| + | <math>\ AB^{-} :=\left\{ {P|\forall P \in AB \wedge \not\in \ AB^{+} \cup A } \right\}</math> --[[Benutzer:RicRic|RicRic]] 12:46, 4. Dez. 2011 (CET) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 4. Dezember 2011, 12:46 Uhr
Definition: Halbgerade 
- Gegeben seien zwei nicht identische Punkte
und 
. Unter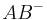 
wollen wir die Menge aller Punkte 
verstehen, die man erhält, wenn man 
über hinaus verlängert.
- Gegeben seien zwei nicht identische Punkte
Geben Sie eine mathematisch korrekte Definition für die Menge dieser Punkte an.
Es seien A und B zwei verschiedene Punkte. Die Halbgerade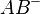 
ist die Punktmenge aller Punkte P, für die gilt:
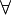P :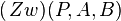 
vereinigt mit {A} --Teufelchen777 01:10, 25. Nov. 2011 (CET)
Vorausgesetzt die Definition aus Aufg. 7.6
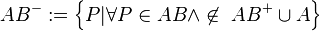--RicRic 12:46, 4. Dez. 2011 (CET)
