Quiz der Woche: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| − | Es sei <math>R</math> ein Äquivalenzrelation auf der Menge <math>M</math>. Wir zerlegen M derart in Teilmengen, dass gilt: Zwei Elemente von M liegen genau dann in derselben Teilmenge, wenn sie in Relation zueinander stehen. | + | Es sei <math>R</math> ein Äquivalenzrelation auf der Menge <math>M</math>. Wir zerlegen <math>\ M</math> derart in Teilmengen <math>\ T_1, T_2, T_3, ..., T_n, ...</math>, dass gilt: Zwei Elemente von <math>\ M</math> liegen genau dann in derselben Teilmenge, wenn sie in Relation <math>R</math> zueinander stehen. |
Im folgenden soll bewiesen werden, dass die so gewonnenen Teilmengen von <math>M</math> eine Klasseneinteilung von <math>M</math> sind. Ergänzen Sie dementsprechend die folgenden Ausführungen: | Im folgenden soll bewiesen werden, dass die so gewonnenen Teilmengen von <math>M</math> eine Klasseneinteilung von <math>M</math> sind. Ergänzen Sie dementsprechend die folgenden Ausführungen: | ||
| Zeile 20: | Zeile 20: | ||
(S) <math>R</math> ist { symmetrisch } | (S) <math>R</math> ist { symmetrisch } | ||
(T) <math>R</math> ist { transitiv } | (T) <math>R</math> ist { transitiv } | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</quiz> | </quiz> | ||
Version vom 13. Mai 2010, 22:10 Uhr
Es sei 
ein Äquivalenzrelation auf der Menge 
. Wir zerlegen 
derart in Teilmengen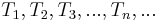 
, dass gilt: Zwei Elemente von liegen genau dann in derselben Teilmenge, wenn sie in Relation zueinander stehen.
Im folgenden soll bewiesen werden, dass die so gewonnenen Teilmengen von eine Klasseneinteilung von sind. Ergänzen Sie dementsprechend die folgenden Ausführungen:
