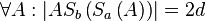Lösungen WiSe 2011/12 - Serie 05: Unterschied zwischen den Versionen
HecklF (Diskussion | Beiträge) (→Aufgabe 5.1) |
HecklF (Diskussion | Beiträge) (→Aufgabe 5.3) |
||
| Zeile 22: | Zeile 22: | ||
# Die Identität ist eine Verschiebung. | # Die Identität ist eine Verschiebung. | ||
| − | + | <br /> | |
| + | Für diejenigen, die an die Ästhetik der Mathematik appelieren, sei gesagt, dass sie bitte nicht mehr weiterlesen sollen. Es wird nicht schön. Für euch sei gesagt, dass die Identität durch Spiegelung an zwei identischen Geraden hergestellt werden kann. Das sollte genügen und ist unmittelbar einleuchtend.<br /> | ||
| + | Diejenigen, die sich immer schon mit der Thematik 'Wie schaffe ich es, einfache und unmittelbar einleuchtende Dinge kompliziert darzustellen und dabei ohne Rücksicht auf Verluste vorzugehen, der hole sich bitte noch ein Bier, ein paar Chips, lehnt sich in seinem Sessel gemütlich zurück und lässt den Wahnsinn einfach vor seinen Augen geschehen.<br /> | ||
| + | LIGHT OFF - SPOT ON! | ||
| + | Wir setzen logischerweise ebene Geometrie voraus.<br /> | ||
| + | Wir haben gegeben: Zwei parallele Geraden a und b. Ferner betrachten wir alle beliebigen Punkte P der Ebene.<br /> | ||
| + | Behauptung: Die Identität ist eine Verschiebung.<br /> | ||
| + | Es gilt also zu zeigen, dass für jeden Punkt P gilt: <math>\forall P \in \epsilon: S_a(S_b(P)) \equiv P</math> | ||
| + | |||
| + | |||
| + | Es gelte: <math>S_a(S_b(P))= P'</math> | ||
| + | Wir werden keine Fallunterscheidung durchführen, da es für unsere Beweisführung (fast) keine Rolle spielt, ob P auf a oder b liegt, da wir uns alle Punkte anschauen und für alle Punkte gleichermaßen den Beweis führen. Ein Punkt alleine würde zum Nachweis der Identität so und so nicht reichen. | ||
| + | |||
| + | Wenn P an der Geraden a gespiegelt wird, dann gilt nach der Definition der Spiegelung, dass a die Mittelsenkrechten von <math>\overline{PP'} </math> ist. Nach der gleichen Definition gilt aber auch, dass die Abbildung von P' auf P genau dann zustande kommt, wenn eine Gerade g Mittelsenkrechten von <math>\overline{PP'} </math> ist. | ||
| + | Aus diesen beiden Punkten folgt: <math>a\equiv b \Leftrightarrow S_b o S_a = id.</math> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | Vielen Dank für die Aufmerksamkeit :-). | ||
| + | <quiz> | ||
| + | {Ich bin ein Freund der ästhetischen Mathematik und hätte mich auch mit der ersten Lösung zu frieden gegeben, habe aber gegen alle Warnungen weitergelesen} | ||
| + | - JA | ||
| + | {erwischt :-)} | ||
| + | + NEIN | ||
| + | {gut, dann hat sich die Arbeit wenigstens gelohnt :-)} | ||
| + | </quiz> | ||
| + | --[[Benutzer:HecklF|Flo60]] 21:29, 30. Nov. 2011 (CET) | ||
| + | |||
| + | |||
| + | # Wenn die beiden Spiegelgeraden <math>a</math> und <math>b</math> den Abstand <math>d</math> zueinander haben, dann gilt <math>\forall A: \left|A S_b \left( S_a \left( A \right) \right)\right| =2d</math> | ||
[[Kategorie:Elementargeometrie]] | [[Kategorie:Elementargeometrie]] | ||
Version vom 30. November 2011, 21:29 Uhr
Aufgabe 5.1
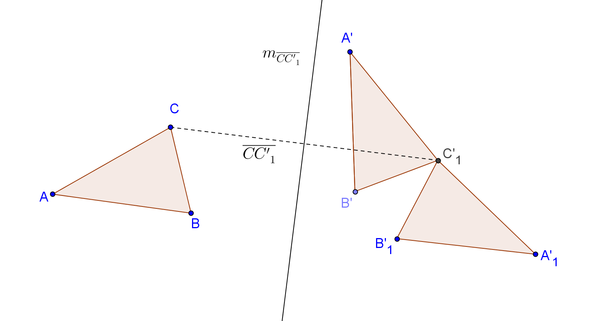
Es sei Fehler beim Parsen(Syntaxfehler): \overline{A'B'C'_1
das Bild vonbei einer Bewegung
.
Fehler beim Parsen(Syntaxfehler): \overline{A'_1B'_1C'_1
sei das Bild vonbei der Spiegelung an der Mittelsenkrechten von
.
Beweisen Sie:
Die Mittelsenkrechte von 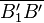 geht durch den Punkt
geht durch den Punkt 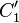 .
.
Die Mittelsenkrechte von 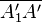 geht durch den Punkt
geht durch den Punkt 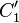 .
.

Aufgabe 5.2
Das Bild aus Aufgabe 5.1 suggeriert, dass die Mittelsenkrechten von 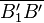 und
und 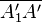 identisch sind. Zeigen Sie mittels einer Skizze, dass es Fälle gibt, in denen dieselben Voraussetzungen wie in Aufgabe 5.1 gelten, die genannten beiden Mittelsenkrechten jedoch nicht identisch sind.
identisch sind. Zeigen Sie mittels einer Skizze, dass es Fälle gibt, in denen dieselben Voraussetzungen wie in Aufgabe 5.1 gelten, die genannten beiden Mittelsenkrechten jedoch nicht identisch sind.
Aufgabe 5.3
Definition: (Verschiebung)
- Die Nacheinanderausführung zweier Geradenspiegelungen
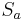 und
und 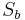 mit
mit 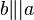 heißt Verschiebung.
heißt Verschiebung.
- Die Nacheinanderausführung zweier Geradenspiegelungen
Beweisen Sie:
- Die Identität ist eine Verschiebung.
Für diejenigen, die an die Ästhetik der Mathematik appelieren, sei gesagt, dass sie bitte nicht mehr weiterlesen sollen. Es wird nicht schön. Für euch sei gesagt, dass die Identität durch Spiegelung an zwei identischen Geraden hergestellt werden kann. Das sollte genügen und ist unmittelbar einleuchtend.
Diejenigen, die sich immer schon mit der Thematik 'Wie schaffe ich es, einfache und unmittelbar einleuchtende Dinge kompliziert darzustellen und dabei ohne Rücksicht auf Verluste vorzugehen, der hole sich bitte noch ein Bier, ein paar Chips, lehnt sich in seinem Sessel gemütlich zurück und lässt den Wahnsinn einfach vor seinen Augen geschehen.
LIGHT OFF - SPOT ON!
Wir setzen logischerweise ebene Geometrie voraus.
Wir haben gegeben: Zwei parallele Geraden a und b. Ferner betrachten wir alle beliebigen Punkte P der Ebene.
Behauptung: Die Identität ist eine Verschiebung.
Es gilt also zu zeigen, dass für jeden Punkt P gilt: 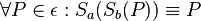
Es gelte: 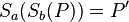 Wir werden keine Fallunterscheidung durchführen, da es für unsere Beweisführung (fast) keine Rolle spielt, ob P auf a oder b liegt, da wir uns alle Punkte anschauen und für alle Punkte gleichermaßen den Beweis führen. Ein Punkt alleine würde zum Nachweis der Identität so und so nicht reichen.
Wir werden keine Fallunterscheidung durchführen, da es für unsere Beweisführung (fast) keine Rolle spielt, ob P auf a oder b liegt, da wir uns alle Punkte anschauen und für alle Punkte gleichermaßen den Beweis führen. Ein Punkt alleine würde zum Nachweis der Identität so und so nicht reichen.
Wenn P an der Geraden a gespiegelt wird, dann gilt nach der Definition der Spiegelung, dass a die Mittelsenkrechten von 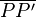 ist. Nach der gleichen Definition gilt aber auch, dass die Abbildung von P' auf P genau dann zustande kommt, wenn eine Gerade g Mittelsenkrechten von
ist. Nach der gleichen Definition gilt aber auch, dass die Abbildung von P' auf P genau dann zustande kommt, wenn eine Gerade g Mittelsenkrechten von 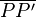 ist.
Aus diesen beiden Punkten folgt:
ist.
Aus diesen beiden Punkten folgt: 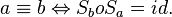
Vielen Dank für die Aufmerksamkeit :-).
--Flo60 21:29, 30. Nov. 2011 (CET)
- Wenn die beiden Spiegelgeraden
 und
und  den Abstand
den Abstand  zueinander haben, dann gilt
zueinander haben, dann gilt