Lösungen WiSe 2011/12 - Serie 05
Inhaltsverzeichnis[Verbergen] |
Aufgabe 5.1
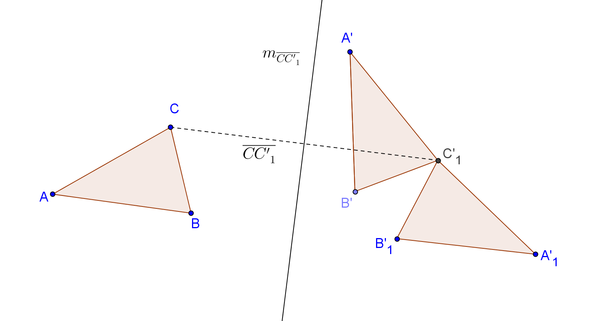
Es sei Fehler beim Parsen(Syntaxfehler): \overline{A'B'C'_1
das Bild vonbei einer Bewegung
.
Fehler beim Parsen(Syntaxfehler): \overline{A'_1B'_1C'_1
sei das Bild vonbei der Spiegelung an der Mittelsenkrechten von
.
Beweisen Sie:
Die Mittelsenkrechte von  geht durch den Punkt
geht durch den Punkt  .
.
Die Mittelsenkrechte von  geht durch den Punkt
geht durch den Punkt 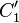 .
.

Aufgabe 5.2
Das Bild aus Aufgabe 5.1 suggeriert, dass die Mittelsenkrechten von 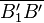 und
und 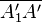 identisch sind. Zeigen Sie mittels einer Skizze, dass es Fälle gibt, in denen dieselben Voraussetzungen wie in Aufgabe 5.1 gelten, die genannten beiden Mittelsenkrechten jedoch nicht identisch sind.
identisch sind. Zeigen Sie mittels einer Skizze, dass es Fälle gibt, in denen dieselben Voraussetzungen wie in Aufgabe 5.1 gelten, die genannten beiden Mittelsenkrechten jedoch nicht identisch sind.
Aufgabe 5.3
Definition: (Verschiebung)
- Die Nacheinanderausführung zweier Geradenspiegelungen
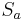 und
und 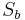 mit
mit 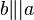 heißt Verschiebung.
heißt Verschiebung.
- Die Nacheinanderausführung zweier Geradenspiegelungen
Beweisen Sie:
- Die Identität ist eine Verschiebung.
Für diejenigen, die an die Ästhetik der Mathematik appelieren, sei gesagt, dass sie bitte nicht mehr weiterlesen sollen. Es wird nicht schön. Für euch sei gesagt, dass die Identität durch Spiegelung an zwei identischen Geraden hergestellt werden kann. Das sollte genügen und ist unmittelbar einleuchtend.
Diejenigen, die sich immer schon mit der Thematik 'Wie schaffe ich es, einfache und unmittelbar einleuchtende Dinge kompliziert darzustellen und dabei ohne Rücksicht auf Verluste vorzugehen, der hole sich bitte noch ein Bier, ein paar Chips, lehnt sich in seinem Sessel gemütlich zurück und lässt den Wahnsinn einfach vor seinen Augen geschehen.
LIGHT OFF - SPOT ON!
Wir setzen logischerweise ebene Geometrie voraus.
Wir haben gegeben: Zwei parallele Geraden a und b. Ferner betrachten wir alle beliebigen Punkte P der Ebene.
Behauptung: Die Identität ist eine Verschiebung.
Es gilt also zu zeigen, dass für jeden Punkt P gilt: 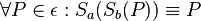
Es gelte: 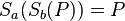 Wir werden keine Fallunterscheidung durchführen, da es für unsere Beweisführung (fast) keine Rolle spielt, ob P auf a oder b liegt, da wir uns alle Punkte anschauen und für alle Punkte gleichermaßen den Beweis führen. Ein Punkt alleine würde zum Nachweis der Identität so und so nicht reichen.
Wir werden keine Fallunterscheidung durchführen, da es für unsere Beweisführung (fast) keine Rolle spielt, ob P auf a oder b liegt, da wir uns alle Punkte anschauen und für alle Punkte gleichermaßen den Beweis führen. Ein Punkt alleine würde zum Nachweis der Identität so und so nicht reichen.
Wenn P an der Geraden a gespiegelt wird, dann gilt nach der Definition der Spiegelung, dass a die Mittelsenkrechten von 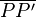 ist. Nach der gleichen Definition gilt aber auch, dass die Abbildung von P' auf P genau dann zustande kommt, wenn eine Gerade g Mittelsenkrechten von
ist. Nach der gleichen Definition gilt aber auch, dass die Abbildung von P' auf P genau dann zustande kommt, wenn eine Gerade g Mittelsenkrechten von 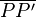 ist. Weil nun
ist. Weil nun 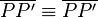 (der Leser überzeuge sich selbst) gilt auch, dass die Menge aller Punkte für die gilt, dass der Abstand zu den Endpunkten der Strecke
(der Leser überzeuge sich selbst) gilt auch, dass die Menge aller Punkte für die gilt, dass der Abstand zu den Endpunkten der Strecke 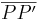 identisch zu sich selbst ist.
Aus diesen Punkten folgt:
identisch zu sich selbst ist.
Aus diesen Punkten folgt: 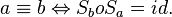
Vielen Dank für die Aufmerksamkeit :-).
- Ich grins mal zurück =) und geb zu: Ich hab's überhaupt nicht verstanden, außer vielleicht
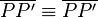 . Dass der Beweis (deine Worte)
. Dass der Beweis (deine Worte)
- Ich grins mal zurück =) und geb zu: Ich hab's überhaupt nicht verstanden, außer vielleicht
einfache und unmittelbar einleuchtende Dinge kompliziert
- darstellt, rettet dich nicht davor, dass ich ihn gern verstehen würde. ;-)
- Ich versuch mal, ne schlaue Frage zu stellen:
- Warum sprichst du nur von
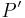 wobei gilt
wobei gilt 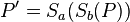 ? Was ist mit dem Punkt, der nach der ersten Spiegelung entsteht, also hier
? Was ist mit dem Punkt, der nach der ersten Spiegelung entsteht, also hier 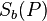 ? Inwiefern kannst du die Definition der Spiegelung hier auf die Nacheinanderausführung von zwei Spiegelungen anwenden?
? Inwiefern kannst du die Definition der Spiegelung hier auf die Nacheinanderausführung von zwei Spiegelungen anwenden?
- --Sternchen 21:26, 1. Dez. 2011 (CET)
@ Sternchen: Zu deiner ersten Anmerkung bzgl. 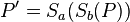 : Hier hast du natürlich vollkommen recht. Ich habe es oben geändert, es muss natürlich lauten
: Hier hast du natürlich vollkommen recht. Ich habe es oben geändert, es muss natürlich lauten 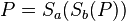 und nicht P'.
und nicht P'.
Das zweite versuche ich kurz zu erklären: Ich habe tatsächlich nicht mit der NAF gearbeitet - gar nicht. Wir haben jedoch irgendwann definiert (oder uns darüber zumindest mal Gedanken gemacht :-)), dass die NAF nichts anderes ist, als zwei nacheinander ausgeführte Bewegungen. In diesem Falle sind es zwei Spiegelungen (logisch). Ich wende die Definition der Spiegelung nicht explizit auf die NAF an. Die Definition sagt mir nur, dass die Identität genau dann hergestellt wird, wenn die beiden Spiegelgeraden identisch sind. Da ich nun zwei Spiegelungen hintereinander ausführe, fasse ich das unter den Begriff der NAF zusammen, da das ja passt.
Im Übrigen muss ich hier noch zugeben, dass der Beweis (trotz aller Ausschmückung (oder vielleicht gerade deshalb) nicht ganz sauber ist. Ich habe nämlich eigentlich gezeigt, dass die Verschiebung für den speziellen Fall, dass 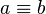 ist, die Identität ist. Das ist aber wenn man es ganz genau nimmt nicht das, was man zeigen sollte. Aus diesem Grunde, werde ich es weiter unten nochmal genauer und vor allem ohne Ausschmückung versuchen. --Flo60 22:38, 4. Dez. 2011 (CET)
ist, die Identität ist. Das ist aber wenn man es ganz genau nimmt nicht das, was man zeigen sollte. Aus diesem Grunde, werde ich es weiter unten nochmal genauer und vor allem ohne Ausschmückung versuchen. --Flo60 22:38, 4. Dez. 2011 (CET)
--Flo60 21:29, 30. Nov. 2011 (CET)
- Wenn die beiden Spiegelgeraden
 und
und  den Abstand
den Abstand  zueinander haben, dann gilt
zueinander haben, dann gilt 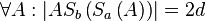
Dafür ist die umso schwieriger - glaube ich :-).
Ich denke, wir müssen drei Fälle unterscheiden.
Voraussetzung: Zwei parallele Geraden a und b, mit dem Abstand d. Punkt A
Behauptung: 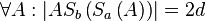
Wir gönnen uns zur besseren Beschreibung der einzelnen Fälle noch eine Senkrechte s mit der Eigenschaft: 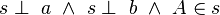 . Ferner gilt:
. Ferner gilt: 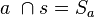 und
und 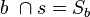
Fallunterscheidung:
Fall I: 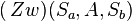
Fall II: 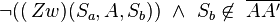
Fall III: 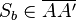
Skizze:
Für Fall I gilt:
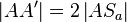 .
.
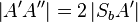 , weil Spiegelung gleich Bewegung und somit abstandserhaltend
, weil Spiegelung gleich Bewegung und somit abstandserhaltend
Demnach gilt: 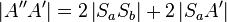 Hier könnte man noch mit Halbebenen argumentieren - ich denke aber die Argumentation Mittelsenkrechtenkriterium müsste reichen, weil ja A' dadurch nicht mehr in der Halbebene
Hier könnte man noch mit Halbebenen argumentieren - ich denke aber die Argumentation Mittelsenkrechtenkriterium müsste reichen, weil ja A' dadurch nicht mehr in der Halbebene 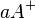 liegen kann und demnach wird
liegen kann und demnach wird 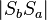 komplett gespiegelt.
komplett gespiegelt.
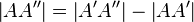
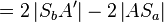
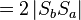 Nach vorherigen Schritten. [Änderung: --Sternchen 21:10, 1. Dez. 2011 (CET)]
Nach vorherigen Schritten. [Änderung: --Sternchen 21:10, 1. Dez. 2011 (CET)]
Begründet wird natürlich immer mit dem Mittelsenkrechtenkriterium und der Definiton von Spiegelung.
Die restlichen Fälle werden analog ausgeführt und durch rechnerische Begründungen beschränkt. Durch diese Fallunterscheidung ist es relativ einfach diese Tatsache nahezulegen, jedoch schreiberisch arg aufwendig und irreführend. Vielleicht gibt es eine allgemeinere Lösung. --Flo60 22:48, 30. Nov. 2011 (CET)
Aufgabe 5.3 - Teil I: Versuch 2
Definition: (Verschiebung)
- Die Nacheinanderausführung zweier Geradenspiegelungen
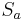 und
und 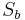 mit
mit 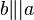 heißt Verschiebung.
heißt Verschiebung.
- Die Nacheinanderausführung zweier Geradenspiegelungen
Beweisen Sie:
- Die Identität ist eine Verschiebung.
Voraussetzung: Identität, d. h. 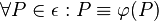
Behauptung:  ist die NAF zweier Geradenspiegelungen a und b mit a || b
ist die NAF zweier Geradenspiegelungen a und b mit a || b
z. z.:
(1)  ist NAF zweier Geradenspiegelungen.
ist NAF zweier Geradenspiegelungen.
(2) Für alle Punkte P gibt es eine Verschiebung, die 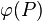 auf P abbildet.
auf P abbildet.
Wir können zwei Sätze voraussetzen:
- Die Bewegung von drei nichtkollinearen Punkten ist eindeutig festgelegt.
- Für drei nichtkollineare Punkte A, B, C gilt:
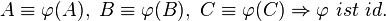 (genau genommen haben wir es hier mit einer Äquivalenz zu tun. Begründen kann man das mit dem vorherig genannten Satz.
(genau genommen haben wir es hier mit einer Äquivalenz zu tun. Begründen kann man das mit dem vorherig genannten Satz.
Seien A, B, C drei nichtkollineare Punkte,a und b zwei Spiegelgeraden.
Beweisteil (1): Identität ist NAF zweier Geradenspiegelungen
Nehmen wir an, durch eine Geradenspiegelung wird die Identität hergestellt.
Nach Definition der Spiegelung wird bei der Spiegelung ein Punkt nur dann auf sich selbst abgebildet, wenn er auf der Spiegelgeraden liegt. Demnach müssen alle Punkte auf der Spiegelgeraden liegen. Dies ist aber ein Widerspruch zu unserer Voraussetzung, dass A, B und C nicht kollinear sind. Annahme ist zu verwerfen.
Eine weitere Ausführung benötigen wir hier nicht mehr (z. B. zu zeigen, dass auch drei oder mehr Geradenspiegelungen nicht die Identität hervorbringen), da dies im zweiten Beweisteil mitbewiesen wird, d. h. wir zeigen dort, dass wir nach zwei Geradenspiegelungen die Identität herstellen. Es ist ja nicht zu beweisen, dass die NAF von mindestens zwei parallelen Geraden eine Verschiebung ist.
Beweisteil (2): a und b sind parallel
Annahme: a ist nicht parallel zu b.
| Nummer | Beweisschritt | Begründung |
|---|---|---|
| 1 | 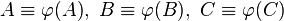 |
Voraussetzung, Identität |
| 2 | Nach Spiegelung an a entstehen die Punkte A', B' und C' für die gilt, dass a die Mittelsenkrechte von 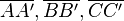 oder dass zwei Punkte auf a liegen oder dass zwei Punkte auf a liegen |
Definition Spiegelung |
| 3 | a und b sind nicht parallel | Nach Annahme |
| 4 | Durch Spiegelung an b werden die Punkte A', B' und C' auf A, B und C abgebildet | Voraussetzung der Identität und (1) |
| 5 | Weil 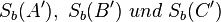 gleich A, B und C ist, gilt, dass b Mittelsenkrechten von gleich A, B und C ist, gilt, dass b Mittelsenkrechten von 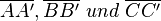 ist. ist. |
(4) |
| 6 | 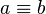 |
(5), (2) und Existenz und Eindeutigkeit der Mittelsenkrechten |
| 7 | Wiederspruch zur Annahme. Annahme ist somit zu verwerfen! | (3) und 6 |
q. e. d. Die Identität ist eine Verschiebung.--Flo60 22:45, 4. Dez. 2011 (CET)

