Quiz der Woche 11 (WS 11/12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „{| class="wikitable" |- | <quiz> { Die nebenstehenden Abbildungen sind im Rahmen der Veranstaltung: "Vorbereitung auf die Klausur mit Hilfe eines Classroomprese…“)
 
 
Zeile 46: Zeile 46:
 
    
 
    
 
|}
 
|}
 +
 +
 +
Bezogen auf Beweis eins:
 +
Möchte ich bei der Beweisidee bleiben, kann ich doch den Beweis so berichtigen, oder?<br />
 +
Vor.: <math>\overline{AC} \tilde {=} \overline{BC}</math> <br />
 +
Beh.: <math>\alpha \tilde {=} \beta</math> <br />
 +
Beweis:
 +
 +
{| class="wikitable sortable"
 +
!Überschrift 1!!Überschrift 2
 +
|-
 +
| (1) <math>\overline{AC} \tilde {=} \overline{BC}</math> <br />|| Vorr
 +
|-
 +
| (2) <math>\exists M: M\in \overline{AB} \wedge \overline{AM} \tilde {=} \overline{BM}</math>  || Existenz und Eindeutigkeit des Mittelpunkts einer Strecke
 +
|-
 +
| (3) <math>\exists m: m \perp \overline{AB} \wedge M \in m</math> || Existenz und Eindeutigkeit der Mittelsenkrechten, (2)
 +
|-
 +
| (4) <math>C\in m</math> || Mittelsenkrechtenkriterium (1)
 +
|-
 +
| (5) <math>\overline{CM} = \overline{CM}</math>  || trivial
 +
|-
 +
| (6) <math>\overline{ACM} \tilde {=} \overline{BCM}</math>  || SWS, (5),(3),(1)
 +
|-
 +
| (7) <math>\alpha \tilde {=} \beta</math>  || (6)
 +
|-
 +
| q.e.d. || --[[Benutzer:RicRic|RicRic]] 20:22, 5. Jan. 2012 (CET)
 +
|}
 +
 +
 +
 
[[Category:Einführung_Geometrie]]
 
[[Category:Einführung_Geometrie]]

Aktuelle Version vom 5. Januar 2012, 20:22 Uhr

Pluspunkt für eine richtige Antwort:  
Minuspunkte für eine falsche Antwort:
Ignoriere den Fragen-Koeffizienten:

1. Die nebenstehenden Abbildungen sind im Rahmen der Veranstaltung: "Vorbereitung auf die Klausur mit Hilfe eines Classroompresenters" im letzten Semester entstanden. Bei der Beweisführung wurde jeweils davon ausgegangen, dass der Kongruenzsatz sss unabhängig vom Basiswinkelsatz bereits bewiesen wurde. Beurteilen Sie die aufgeführten Beweisschritte:

Die Voraussetzung ist korrekt notiert.
→ Es steht da eigentlich, dass die beiden Seiten \overline{AC} und \overline{BC} identisch sind, es sind ja aber nicht die gleichen Seiten, sondern die Seiten sind kongruent zueinander bzw. die Länge der Seiten sind gleich.
Die Behauptung ist korrekt notiert.
→ Auch hier das gleiche Problem. Richtig wäre: |\alpha|=|\beta| oder \alpha \cong \beta
Der erste Beweisschritt und seine Begründung ist korrekt.
→ Ja, prima!
Der zweite Beweisschritt und seine Begründung ist korrekt.
→ Die Begründung dieses Schrittes ist nicht ganz richtig. Nur weil wir eine Definition des Mittelpunktes haben, heißt dies ja noch lange nicht, dass dieser auch existiert. Richtige Begründung: Satz über die Existenz und Eindeutigkeit des Mittelpunktes einer Strecke.
Der dritte Beweisschritt und seine Begründung ist korrekt.
→ Dieser Schritt ist erstens nicht notwendig und zweitens so nicht begründbar. Woher wollen Sie denn wissen, dass das hier rechte Winkel sind?
Der vierte Beweisschritt und seine Begründung ist korrekt.
→ Ja, das ist OK!
Der fünfte Beweisschritt und seine Begründung ist korrekt.
→ Da wir schon gesehen haben, dass der dritte Schritt fehlerhaft ist, ist auch dieser fünfte Schritt hinfällig. Sinnvoll wäre an dieser Stelle mit dem Kongruenzsatz sss zu argumentieren, da wir je drei paarweise kongruente Seiten haben.
Der sechste Beweisschritt und seine Begründung ist korrekt.
→ Wären die Beweisschritte im Vorfeld richtig gewesen, d. h. die Dreieckskongruenz wäre über den Kongruenzsatz sss bewiesen worden, hätte man jetzt diese Schlussfolgerung ziehen können.

Punkte: 0 / 0
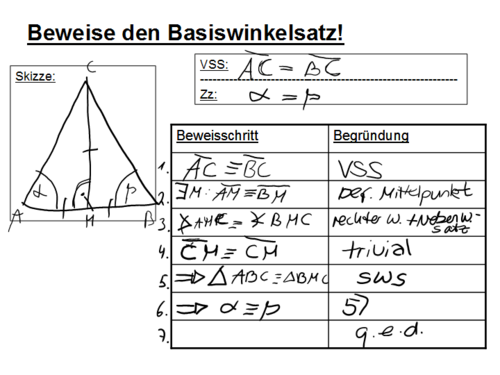
 Bild 076.png
Pluspunkt für eine richtige Antwort:  
Minuspunkte für eine falsche Antwort:
Ignoriere den Fragen-Koeffizienten:

1.

Die Voraussetzung ist korrekt notiert.
→ ja, richtig!
Die Behauptung ist korrekt notiert.
→ auch das stimmt!
Der "nullte" Beweisschritt und seine Begründung ist korrekt.
→ Die Begründung dieses Schrittes ist nicht ganz richtig. Nur weil wir eine Definition des Mittelpunktes haben, heißt dies ja noch lange nicht, dass dieser auch existiert. Richtige Begründung: Satz über die Existenz und Eindeutigkeit des Mittelpunktes einer Strecke.
Der erste Beweisschritt und seine Begründung ist korrekt.
→ Ja, prima!
Der zweite Beweisschritt und seine Begründung ist korrekt.
→ auch das stimmt!
Der dritte Beweisschritt und seine Begründung ist korrekt.
→ ja, das ist OK!
Der vierte Beweisschritt und seine Begründung ist korrekt.
→ in der Begründung fehlt noch der Hinweis auf den Kongruenzsatz sss, auf den man sich hier bezieht.
Der fünfte Beweisschritt und seine Begründung ist korrekt.
→ das stimmt und damit ist die Behauptung gezeigt!

Punkte: 0 / 0
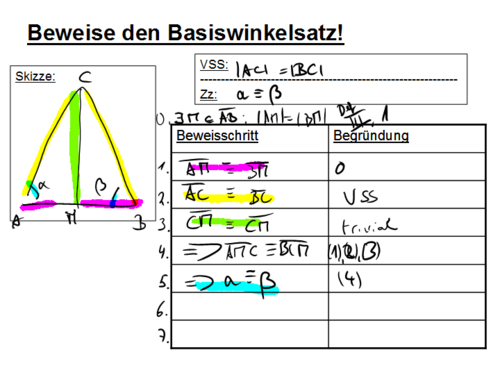
 Bild 077.png


Bezogen auf Beweis eins: Möchte ich bei der Beweisidee bleiben, kann ich doch den Beweis so berichtigen, oder?
Vor.: 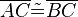\overline{AC} \tilde {=} \overline{BC}
Beh.: 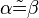\alpha \tilde {=} \beta
Beweis:

Überschrift 1 Überschrift 2
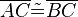(1) \overline{AC} \tilde {=} \overline{BC}
Vorr
(2) 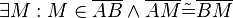\exists M: M\in \overline{AB} \wedge \overline{AM} \tilde {=} \overline{BM} Existenz und Eindeutigkeit des Mittelpunkts einer Strecke
(3) 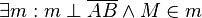\exists m: m \perp \overline{AB} \wedge M \in m Existenz und Eindeutigkeit der Mittelsenkrechten, (2)
(4) 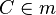C\in m Mittelsenkrechtenkriterium (1)
(5) 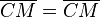\overline{CM} = \overline{CM} trivial
(6) 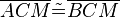\overline{ACM} \tilde {=} \overline{BCM} SWS, (5),(3),(1)
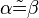(7) \alpha \tilde {=} \beta (6)
q.e.d. --RicRic 20:22, 5. Jan. 2012 (CET)
Von „http://geometrie.zum.de/index.php?title=Quiz_der_Woche_11_(WS_11/12)&oldid=10397“