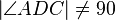Problem der Woche 12 (WS 11/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
RicRic (Diskussion | Beiträge) |
|||
| Zeile 32: | Zeile 32: | ||
Wenn ich die Figur berachte denke ich nicht, dass die Mittelsenkrechten sich in der Figur schneiden, somit entstehen die Dreiecke nicht wie in der Abbildung, sondern eher so<--[[Benutzer:RicRic|RicRic]] 21:31, 12. Jan. 2012 (CET): | Wenn ich die Figur berachte denke ich nicht, dass die Mittelsenkrechten sich in der Figur schneiden, somit entstehen die Dreiecke nicht wie in der Abbildung, sondern eher so<--[[Benutzer:RicRic|RicRic]] 21:31, 12. Jan. 2012 (CET): | ||
<ggb_applet width="1600" height="760" version="4.0" ggbBase64="UEsDBBQACAAIANWrLEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIANWrLEAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vptc+O2Ef58+RUYfui0U0siAL5epctY9mRyM3ZyU7udTJN8gEhIwpkiGJJ6S5MflT/S39QFQFKkZPntfK19HlMgiSUW+zy72AWl4debRYJWPC+ETEcW7tsW4mkkY5HORtaynPYC6+t3Xw1nXM74JGdoKvMFK0eWoyRFPLJCjwWTOOI91yG45/DppMdiYvdiFoYx4Sx2bMdCaFOIt6n8ji14kbGIX0VzvmAXMmKlVjwvy+ztYLBer/u1qr7MZ4PZbNLfFLGFYJppMbKqk7cwXOehNdXixLbx4IfLCzN8T6RFydKIW0iZsBTvvnozXIs0lmu0FnE5B4M97FlozsVsDkYFPlwMlFQGiGQ8KsWKF/Bs61IbXS4yS4uxVPW/MWcoaeyxUCxWIub5yLL7mFDfax8WkrngaVkJ40rpoB5uuBJ8bcZVZ1olgFhKmUyYGhL99hsiNrHRiWqwaQg0nme6bHPPpqYhpnFM4xoZxzzuGFHHyDhGxqEWWolCTBI+sqYsKQBDkU5z4K+5LsptwvV8qhs78/EJ2FSIX0GY2uAoBnS4b9sn6vDgcFTHoGskbmkt8+UjldYqsfcYneSTLKW1UnKbTuIesdO7Q6kx/EGGui2doEr/6+NAI73LzH2N5vrTFHrO/8TE4aCOlWEVHqiYK9nKfUq+KHTAIEd9YHWE6gOCABF1om5T1Q+HuokhhJCnrnzV5epHfCWkOqgWJ6jSLtJsWVYaKyOiRVxrL2XW3AZxCPDdOmICvrPMvBkmbMITWHqvFDIIrVii/FNrmsq0RI2vmXuznGVzERVXvCzhqQJ9ZCt2wUq++Qaki1q3lo1kWnzIZXkmk+UiLRCKZGLXE4Vz3DonO2NkQlsdTrvDbXV4rXP/Vr0SetCy4KBf5kUtzuL4vZLYhRpA+X2abMc5ZzeZFF0zhgO9ig/5MkpELFj6TyBfaVG4oN2irryjXtR9SuqZyDy+2hbgEmjzL55LiAocqjy2NVeu7fXD1l+ggjtiyoGdsNMTBvDQkS7faOOrhhW24TsDZ7mKjtbF+2Isk90tbfMZy8plrnMwzCFXhpyms4Rrv9BLFiS46GYiN1cmSqgZ63qbwVXlHZOZxhpBfBHXBYGqnZhWy6ipNVK2lrG1RONhIm76cUi0hG4nptVS4LJmapWpuDYT27UaUehVwba6waIdXqXLZSrKi/qiFNFNZSo2D3y3XEx44zbdMfFzjTkc7PnV8IbnKU8qNwYyl3JZmKhseXjMI7GAS9NRW6zo+gdMwNyN+Szn9cQTXd8YwNrPGAc9uK2H+iaXi/fp6hp8YW8Cw0E9y2ER5SJTPocmsJTe8J1XxaJgsBLH7edU3IHpkVpxAZ5SQQMRuSznMtcVDCwk0KpwS/gCyhVUavfSHtrAfK4LIYUnkpOPsJY16cP07wiD7ltdTTslS7I5U8VSZXTCtjzvwKDHu5TxPjiAvbYA4joz3GacG7cw84WTDIbT0dRZmADtAm2UUlfFsy5qITH/aupgUwcqW1WMGaVO++4eUeA9BqZ7ADt7/YB5fZ9UgOHPD9j4iwDM04Ap7Z8br9PXj1fP7lOnAswlz4JYJBcLlsYo1QXoB5lsZzK1djUcs9VahhhWEYoYUX6HGFVwGqyWZS0GySGB7IuNNDPSEyMdQQNVUmzUV0pvIcyorylpRuxm0xKKuxvYEha6DCir5K5PvhVxzHWhPLib7Ra+bbqxSzXhLq7S/Y5v/Bi+jztlwWfqqpkIu8ctHz/RRzpmx71gd9b+U0q2Kk6xo72tR5x+4Nv0oKx7Cjn8l9Q8Upj6QyyyRESibBwrUaHwPi2hGuE6HR8WGTecZ6q6+z69zllaqNcwRqZVvDyQiMnLIcLkD7MuOl1GqFcREfQxAakvBf3o5aDfM4srwN/zIeoV3LTvYvegqn+1YMcvCGyAlnY2irXnh7hzOzR+j/te8JqI6OZXvVvdy67jTnY9P0ir//nj7qSp90ENdSCt35SyZFlXAn0fh7Yb2qFPSEApde/LjXdVQti2n5wZP4E3lke72oYG9Y4xkeu/82nCNxrYgx3gMRouYAZjoQiW+R4b0QH+/G74lTUNcvxpgdV9w/AMUaXXrW2zlOmEQfqe6wafJ3SeBDU7gHr6CKinLwTqnimOtsfKJ8AeoA/IZ1q0jiPfLGJ7sHOz3kwP0L+8rzhv76Yun7SbUm+/Z6aZmObTCcBQLVFqkxp0bGpWAD0koRv4df5wq0we2iTo1FPPt326qvJsF/BTA/jlAeCzuwHfz9qzl+Lxbp+6Lvao4xPqA8DmLREg62HiYscOieN4juObhYf2g8D2bI9i6qhX0K9px/AQei8NveMDeuePo3f+Quh1YYd3G7uYBr4TQB3huy513YrcEKoLD9uu7VMIK+9LI/fsWOyKx5ErXgi5UD/7uM2ub+iFKLXDQ35huw8x64XEgxqS+MoZvix+z4/x+/Fx/H58OfwGHX4Dpwpf2+kszkG1ncJ9Ejrejnbn1RJ8LqpftdyafQ/3VWyi5OPT87uZTpcLnoto976ueWxvn0Whvvbd0AlogB3sBuHD6cYH2/dNlgPk6m1xpfaab0rQiaBnZP3pl6Us//aTXPFcEfVvc43+iv6sfkn04+nPf2nOz/W5Efgd/XSCRuqjeWBnjf4mvmt6CTqtvQn8P91cFBfsmv/QdYjqJwAFkDTdfV2uv/61rdoVqwHA1rz8oGo6g+OliHWF9+PpCTr/+Unu1ezej7jX+OxJ7jU+O9zGQ/EEizC1KXF8l+Jndy/Q+SD3Grfc6+xB7qVGfoB7je/7DvC1utf4BJ0duNeg/UWz/g1H9Qu/d/8FUEsHCHeF2qZDCAAAfigAAFBLAQIUABQACAAIANWrLEDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgA1assQHeF2qZDCAAAfigAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAADaCAAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /> | <ggb_applet width="1600" height="760" version="4.0" ggbBase64="UEsDBBQACAAIANWrLEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIANWrLEAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vptc+O2Ef58+RUYfui0U0siAL5epctY9mRyM3ZyU7udTJN8gEhIwpkiGJJ6S5MflT/S39QFQFKkZPntfK19HlMgiSUW+zy72AWl4debRYJWPC+ETEcW7tsW4mkkY5HORtaynPYC6+t3Xw1nXM74JGdoKvMFK0eWoyRFPLJCjwWTOOI91yG45/DppMdiYvdiFoYx4Sx2bMdCaFOIt6n8ji14kbGIX0VzvmAXMmKlVjwvy+ztYLBer/u1qr7MZ4PZbNLfFLGFYJppMbKqk7cwXOehNdXixLbx4IfLCzN8T6RFydKIW0iZsBTvvnozXIs0lmu0FnE5B4M97FlozsVsDkYFPlwMlFQGiGQ8KsWKF/Bs61IbXS4yS4uxVPW/MWcoaeyxUCxWIub5yLL7mFDfax8WkrngaVkJ40rpoB5uuBJ8bcZVZ1olgFhKmUyYGhL99hsiNrHRiWqwaQg0nme6bHPPpqYhpnFM4xoZxzzuGFHHyDhGxqEWWolCTBI+sqYsKQBDkU5z4K+5LsptwvV8qhs78/EJ2FSIX0GY2uAoBnS4b9sn6vDgcFTHoGskbmkt8+UjldYqsfcYneSTLKW1UnKbTuIesdO7Q6kx/EGGui2doEr/6+NAI73LzH2N5vrTFHrO/8TE4aCOlWEVHqiYK9nKfUq+KHTAIEd9YHWE6gOCABF1om5T1Q+HuokhhJCnrnzV5epHfCWkOqgWJ6jSLtJsWVYaKyOiRVxrL2XW3AZxCPDdOmICvrPMvBkmbMITWHqvFDIIrVii/FNrmsq0RI2vmXuznGVzERVXvCzhqQJ9ZCt2wUq++Qaki1q3lo1kWnzIZXkmk+UiLRCKZGLXE4Vz3DonO2NkQlsdTrvDbXV4rXP/Vr0SetCy4KBf5kUtzuL4vZLYhRpA+X2abMc5ZzeZFF0zhgO9ig/5MkpELFj6TyBfaVG4oN2irryjXtR9SuqZyDy+2hbgEmjzL55LiAocqjy2NVeu7fXD1l+ggjtiyoGdsNMTBvDQkS7faOOrhhW24TsDZ7mKjtbF+2Isk90tbfMZy8plrnMwzCFXhpyms4Rrv9BLFiS46GYiN1cmSqgZ63qbwVXlHZOZxhpBfBHXBYGqnZhWy6ipNVK2lrG1RONhIm76cUi0hG4nptVS4LJmapWpuDYT27UaUehVwba6waIdXqXLZSrKi/qiFNFNZSo2D3y3XEx44zbdMfFzjTkc7PnV8IbnKU8qNwYyl3JZmKhseXjMI7GAS9NRW6zo+gdMwNyN+Szn9cQTXd8YwNrPGAc9uK2H+iaXi/fp6hp8YW8Cw0E9y2ER5SJTPocmsJTe8J1XxaJgsBLH7edU3IHpkVpxAZ5SQQMRuSznMtcVDCwk0KpwS/gCyhVUavfSHtrAfK4LIYUnkpOPsJY16cP07wiD7ltdTTslS7I5U8VSZXTCtjzvwKDHu5TxPjiAvbYA4joz3GacG7cw84WTDIbT0dRZmADtAm2UUlfFsy5qITH/aupgUwcqW1WMGaVO++4eUeA9BqZ7ADt7/YB5fZ9UgOHPD9j4iwDM04Ap7Z8br9PXj1fP7lOnAswlz4JYJBcLlsYo1QXoB5lsZzK1djUcs9VahhhWEYoYUX6HGFVwGqyWZS0GySGB7IuNNDPSEyMdQQNVUmzUV0pvIcyorylpRuxm0xKKuxvYEha6DCir5K5PvhVxzHWhPLib7Ra+bbqxSzXhLq7S/Y5v/Bi+jztlwWfqqpkIu8ctHz/RRzpmx71gd9b+U0q2Kk6xo72tR5x+4Nv0oKx7Cjn8l9Q8Upj6QyyyRESibBwrUaHwPi2hGuE6HR8WGTecZ6q6+z69zllaqNcwRqZVvDyQiMnLIcLkD7MuOl1GqFcREfQxAakvBf3o5aDfM4srwN/zIeoV3LTvYvegqn+1YMcvCGyAlnY2irXnh7hzOzR+j/te8JqI6OZXvVvdy67jTnY9P0ir//nj7qSp90ENdSCt35SyZFlXAn0fh7Yb2qFPSEApde/LjXdVQti2n5wZP4E3lke72oYG9Y4xkeu/82nCNxrYgx3gMRouYAZjoQiW+R4b0QH+/G74lTUNcvxpgdV9w/AMUaXXrW2zlOmEQfqe6wafJ3SeBDU7gHr6CKinLwTqnimOtsfKJ8AeoA/IZ1q0jiPfLGJ7sHOz3kwP0L+8rzhv76Yun7SbUm+/Z6aZmObTCcBQLVFqkxp0bGpWAD0koRv4df5wq0we2iTo1FPPt326qvJsF/BTA/jlAeCzuwHfz9qzl+Lxbp+6Lvao4xPqA8DmLREg62HiYscOieN4juObhYf2g8D2bI9i6qhX0K9px/AQei8NveMDeuePo3f+Quh1YYd3G7uYBr4TQB3huy513YrcEKoLD9uu7VMIK+9LI/fsWOyKx5ErXgi5UD/7uM2ub+iFKLXDQ35huw8x64XEgxqS+MoZvix+z4/x+/Fx/H58OfwGHX4Dpwpf2+kszkG1ncJ9Ejrejnbn1RJ8LqpftdyafQ/3VWyi5OPT87uZTpcLnoto976ueWxvn0Whvvbd0AlogB3sBuHD6cYH2/dNlgPk6m1xpfaab0rQiaBnZP3pl6Us//aTXPFcEfVvc43+iv6sfkn04+nPf2nOz/W5Efgd/XSCRuqjeWBnjf4mvmt6CTqtvQn8P91cFBfsmv/QdYjqJwAFkDTdfV2uv/61rdoVqwHA1rz8oGo6g+OliHWF9+PpCTr/+Unu1ezej7jX+OxJ7jU+O9zGQ/EEizC1KXF8l+Jndy/Q+SD3Grfc6+xB7qVGfoB7je/7DvC1utf4BJ0duNeg/UWz/g1H9Qu/d/8FUEsHCHeF2qZDCAAAfigAAFBLAQIUABQACAAIANWrLEDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgA1assQHeF2qZDCAAAfigAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAADaCAAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /> | ||
| + | |||
| + | |||
| + | |||
| + | Ich denke so sollte die Vor. und Beh. für den Beweis aussehen | ||
| + | |||
| + | Vor.: Viereck <math>\overline{ABCD}</math> mit <math>\left|\angle BCD \right| = 90</math> und <math>\overline{BC} =\overline{AD}</math>.<br /> | ||
| + | |||
| + | Behauptung: <math>\left|\angle ADC \right|\neq 90</math> | ||
[[Kategorie:Einführung_Geometrie]] | [[Kategorie:Einführung_Geometrie]] | ||
Version vom 12. Januar 2012, 22:30 Uhr
Entdecken Sie den Fehler:
Beweis dafür, dass alle Winkel das Maß 90 haben:
Vor.: Viereck  mit
mit 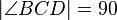 ;
; 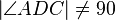 und
und 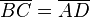 .
.
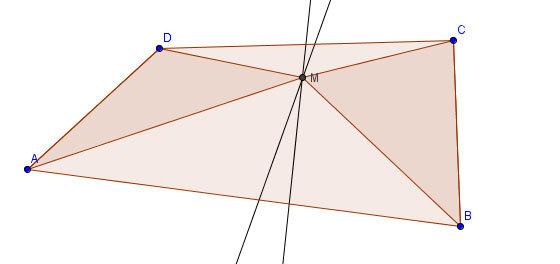
Beh.: 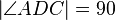
Beweis:
| Beweisschritt | Begründung |
(1)  und und  sind Mittelsenkrechten von sind Mittelsenkrechten von  und und  |
Existenz und Eindeutigkeit der Mittelsenkrechten |
(2) 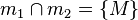 |
Genau ein Schnittpunkt von zwei nicht identischen und nicht parallelen Geraden |
(3) 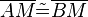 |
(1), (2), Mittelsenkrechtenkriterium |
(4) 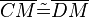 |
(1), (2), Mittelsenkrechtenkriterium |
(5) 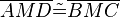 |
Vor., (3), (4), sss-Kongruenzsatz |
(6) 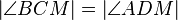 |
(5) |
(7) 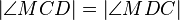 |
Basiswinkelsatz |
(8) 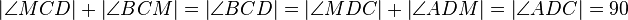 |
(6), (7), Winkeladditionsaxiom, Rechnen in R |
Erst mal wird etwas behaupet was bereis in der Vorraussetung negiert ist. Vorr.: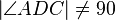 ; Beh.:
; Beh.: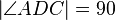 . Wie soll dies Möglich sein es entsteht direkt ein Wiederspruch zu Vorr.
Wenn ich die Figur berachte denke ich nicht, dass die Mittelsenkrechten sich in der Figur schneiden, somit entstehen die Dreiecke nicht wie in der Abbildung, sondern eher so<--RicRic 21:31, 12. Jan. 2012 (CET):
. Wie soll dies Möglich sein es entsteht direkt ein Wiederspruch zu Vorr.
Wenn ich die Figur berachte denke ich nicht, dass die Mittelsenkrechten sich in der Figur schneiden, somit entstehen die Dreiecke nicht wie in der Abbildung, sondern eher so<--RicRic 21:31, 12. Jan. 2012 (CET):
Ich denke so sollte die Vor. und Beh. für den Beweis aussehen
Vor.: Viereck  mit
mit 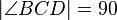 und
und 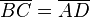 .
.
Behauptung: