Lösung von Aufg. 14.4 (WS 11/12: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Schauen Sie sich das nachfolgende Applet an und bewegen Sie die Figur am Punkt Z.<br /> a) Welche Bedingung ergibt sich für den dargestellten Winkel <math>\angle…“) |
|||
| Zeile 1: | Zeile 1: | ||
Schauen Sie sich das nachfolgende Applet an und bewegen Sie die Figur am Punkt Z.<br /> | Schauen Sie sich das nachfolgende Applet an und bewegen Sie die Figur am Punkt Z.<br /> | ||
a) Welche Bedingung ergibt sich für den dargestellten Winkel <math>\angle MAB</math>, wenn die Gerade ''g'' zur Tangente am Kreis ''k'' im Punkt ''A'' wird?<br /><br /> | a) Welche Bedingung ergibt sich für den dargestellten Winkel <math>\angle MAB</math>, wenn die Gerade ''g'' zur Tangente am Kreis ''k'' im Punkt ''A'' wird?<br /><br /> | ||
| + | Der Winkel <math>\angle MAB</math> wird zum rechten Winkel, <math>MAB \perp g</math><br> | ||
b) Ergänzen Sie mit der Erkenntnis aus a) den folgenden Satz: Wenn eine Gerade ''g'' Tangente an einem Kreis ''k'' im Berührpunkt ''A'' ist, dann ...<br /><br /> | b) Ergänzen Sie mit der Erkenntnis aus a) den folgenden Satz: Wenn eine Gerade ''g'' Tangente an einem Kreis ''k'' im Berührpunkt ''A'' ist, dann ...<br /><br /> | ||
c) Beweisen Sie den Satz aus b) indirekt.<br /><br /> | c) Beweisen Sie den Satz aus b) indirekt.<br /><br /> | ||
Version vom 30. Januar 2012, 10:50 Uhr
Schauen Sie sich das nachfolgende Applet an und bewegen Sie die Figur am Punkt Z.
a) Welche Bedingung ergibt sich für den dargestellten Winkel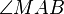 
, wenn die Gerade g zur Tangente am Kreis k im Punkt A wird?
Der Winkel 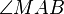wird zum rechten Winkel,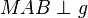 
b) Ergänzen Sie mit der Erkenntnis aus a) den folgenden Satz: Wenn eine Gerade g Tangente an einem Kreis k im Berührpunkt A ist, dann ...
c) Beweisen Sie den Satz aus b) indirekt.
d) Gilt auch die Umkehrung des Satzes aus b)? Beweisen Sie dies.
e) Entwickeln Sie ein Tangentenkriterium aus b) und d)
