Lösung der Aufgaben zur Mengenlehre (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
K (→Mengenlehre) |
|||
| Zeile 1: | Zeile 1: | ||
== Mengenlehre == | == Mengenlehre == | ||
1.<br /> A und B sind identisch. --[[Benutzer:PippiLotta|PippiLotta]] 09:22, 18. Apr. 2012 (CEST) | 1.<br /> A und B sind identisch. --[[Benutzer:PippiLotta|PippiLotta]] 09:22, 18. Apr. 2012 (CEST) | ||
| + | Ich würde sagen B ist Teilmenge von A, da A mehr Zahlen besitzt als B. z.B besitzt B die Zahlen 1,2,3,5 .... nicht. Somit ist B Teilmenge von A.--[[Benutzer:Maliglowka|Maliglowka]] 16:36, 18. Apr. 2012 (CEST) | ||
| + | 2. <br />M1={}<br />M2={}<br />M3={-2}<br />M4={}<br />M5= Wie kann ich Wurzeln schreiben? Wurzel2<br />M6={-2}<br /><br />M1=M2=M4<br />M3=M6--[[Benutzer:PippiLotta|PippiLotta]] 09:22, 18. Apr. 2012 (CEST)<br /> | ||
| − | + | <math>((M1=M2=M4)\neq (M3=M6))\neq M5</math>--[[Benutzer:Maliglowka|Maliglowka]] 16:36, 18. Apr. 2012 (CEST) | |
| − | + | ||
Version vom 18. April 2012, 15:36 Uhr
Mengenlehre
1.
A und B sind identisch. --PippiLotta 09:22, 18. Apr. 2012 (CEST)
Ich würde sagen B ist Teilmenge von A, da A mehr Zahlen besitzt als B. z.B besitzt B die Zahlen 1,2,3,5 .... nicht. Somit ist B Teilmenge von A.--Maliglowka 16:36, 18. Apr. 2012 (CEST)
2.
M1={}
M2={}
M3={-2}
M4={}
M5= Wie kann ich Wurzeln schreiben? Wurzel2
M6={-2}
M1=M2=M4
M3=M6--PippiLotta 09:22, 18. Apr. 2012 (CEST)
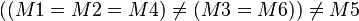--Maliglowka 16:36, 18. Apr. 2012 (CEST)
