Lösung von Aufgabe 1.2 (SoSe 12): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Kommentar von m.g.) |
*m.g.* (Diskussion | Beiträge) (→Kommentar von m.g.) |
||
| Zeile 74: | Zeile 74: | ||
Ich würde sagen, dass (2) korrekt ist. Ein Drachendreieck hat zwei Diagonalen, aber nur eine Diagonale bildet die Symmetrieachse. --[[Benutzer:Honeydukes|Honeydukes]] 22:09, 22. Apr. 2012 (CEST) | Ich würde sagen, dass (2) korrekt ist. Ein Drachendreieck hat zwei Diagonalen, aber nur eine Diagonale bildet die Symmetrieachse. --[[Benutzer:Honeydukes|Honeydukes]] 22:09, 22. Apr. 2012 (CEST) | ||
====Kommentar von m.g.==== | ====Kommentar von m.g.==== | ||
| + | =====Bemerkungen zum Begriff Symmetrieachse==== | ||
| + | {{Definition|(Symmetrieachse)<br /> Es sei <math>\mathbb{F}</math> eine beliebige Figur und <math>s</math> eine Gerade. Wenn bei der Spiegelung an <math>s</math> <math>\mathbb{F}</math> auf sich selbst abgebildet wird, ist <math>s</math> eine Symmetrieachse von <math>\mathbb{F}</math> }} | ||
Eine Gerade ist nicht einfach so eine Symmetrieachse, sondern immer eine Symmetrieachse von irgendeinem anderen geometrischen Objekt. A priori ist jede Gerade eine Symmetrieachse: Es sei <math>g</math> eine Gerade in einer Ebene <math>\varepsilon</math>. Ferner sei <math>P</math> ein Punkt von <math>g</math>. In <math>\varepsilon</math> existiert jetzt <math>s_{Pg}</math>, die Senkrechte in <math>P</math> auf <math>g</math>. Weil bei der Spiegelung an <math>g</math> die Gerade <math>s_{Pg}</math> auf sich selbst abgebildet wird, ist <math>g</math> eine Symmetrieachse von <math>s_{Pg}</math>.<br /> | Eine Gerade ist nicht einfach so eine Symmetrieachse, sondern immer eine Symmetrieachse von irgendeinem anderen geometrischen Objekt. A priori ist jede Gerade eine Symmetrieachse: Es sei <math>g</math> eine Gerade in einer Ebene <math>\varepsilon</math>. Ferner sei <math>P</math> ein Punkt von <math>g</math>. In <math>\varepsilon</math> existiert jetzt <math>s_{Pg}</math>, die Senkrechte in <math>P</math> auf <math>g</math>. Weil bei der Spiegelung an <math>g</math> die Gerade <math>s_{Pg}</math> auf sich selbst abgebildet wird, ist <math>g</math> eine Symmetrieachse von <math>s_{Pg}</math>.<br /> | ||
Version vom 23. April 2012, 17:04 Uhr
Definieren Sie die folgenden Begriffe mathematisch korrekt. Die Begriffe n-Eck, Seite und Ecke eines n-Ecks seien bereits definiert. Beziehen Sie sich auf den nächsthöheren Oberbegriff.
Viereck, Trapez, gleichschenkliges Trapez, Parallelogramm, Drachen, Raute, Rechteck, Quadrat
vielleicht hilft uns hier die Didaktik der Geometrie.... vgl. http://wikis.zum.de/geowiki/Haus_der_Vierecke_%2815.07.2011%29
--Braindead 15:57, 23. Apr. 2012 (CEST)
Inhaltsverzeichnis |
Viereck:
Ein Vieleck mit genau vier Ecken ist ein Viereck.--Oz44oz 23:30, 19. Apr. 2012 (CEST)
FRAGE: Ist Vieleck ein Überbegriff???
Ein Viereck ist ein n-Eck mit n=4. --PippiLotta 14:41, 20. Apr. 2012 (CEST)
- Vieleck und n-Eck sind synonym zu verstehen. Ja, Vieleck/n-Eck ist ein Oberbegriff bzgl. des Begriffs Viereck.--*m.g.* 10:51, 21. Apr. 2012 (CEST)
Quadrat:
Ein Rechteck mit vier gleichlangen Seiten ist ein Quadrat.--Oz44oz 23:36, 19. Apr. 2012 (CEST)
Ein Quadrat ist eine Raute mit einem rechten Innenwinkel.
Raute:
Ein Viereck mit vier kongruenten Seiten ist eine Raute.
Ein Drache mit vier kongruenten Seiten ist eine Raute.
Ein Parallelogramm mit vier kongruenten Seiten ist eine Raute.--Braindead 14:42, 21. Apr. 2012 (CEST)
Ein Viereck dessen gegenüberliegenden Winkel gleich groß sind nennt man Raute.--Michael 20:22, 21. Apr. 2012 (CEST)
Ein Parallelogramm? --PippiLotta 13:53, 22. Apr. 2012 (CEST)
Rechteck:
Ein Viereck mit vier rechten Innenwinkeln ist ein Rechteck.
Ein Parallelogramm mit einem rechten Innenwinkel ist ein Rechteck.
FRAGE: Kann ich auch folgende Definition geben: Ein Rechteck ist ein Parallelogramm mit vier rechten Winkel.
Eine Definition der beiden Definitionen oben besagt, "einem rechten Winkel", aber daraus ergibt sich ja, dass es vier rechte Winkel sein müssen. Ist es nun richtig, wenn man in der Definition schreibt "einen rechten Winkel" oder "vier rechte Winkel"? Welche der beiden Versionen ist korrekt?
über gleichschenkliges Trapez
Ein gleichschenkliges Trapez mit einem rechten Innenwinkel ist ein Rechteck.--Braindead 14:50, 21. Apr. 2012 (CEST)
Trapez:
Ein Viereck mit einem Paar paralleler Gegenseiten ist ein Trapez.--Braindead 14:52, 21. Apr. 2012 (CEST)
Ein Viereck wo immer genau zwei Seiten parallel sind --H2O 18:01, 22. Apr. 2012 (CEST)
@H2O Bei einem Parallelogramm sind je zwei Seiten parallel zueinander... nach deiner Definition ist ein Parallelogramm kein Trapez, da nicht genau zwei Seiten parallel sind.--Tutor Andreas 18:22, 22. Apr. 2012 (CEST)
Parallelogramm:
Ein Parallelogramm ist ein Trapez, bei dem die gegenüberliegenden Seiten parallel sind. --Honeydukes 01:13, 21. Apr. 2012 (CEST)
Anmerkung: Oberbegiff ist Trapez. Unterbegriffe wären u.a. Raute und Rechteck. Frage: Auf die nicht vorhandenen rechten Winkel muss ich bei der Definition nicht eingegen, da der Oberbegriff Trapez diese auch nicht hat. Ist das korrekt? --Honeydukes 01:13, 21. Apr. 2012 (CEST)
Ein Parallelogramm muss ja keinen rechten Winkel haben und Dinge, die nicht relevant sind, sollten in einer Definition auch nicht vorkommen. Ich hoffe, dass ich deine Frage richtig verstanden habe, wenn nicht, dann einfach nochmal anders formulieren.--Tutor Andreas 18:34, 22. Apr. 2012 (CEST)
Danke. --Honeydukes 22:09, 22. Apr. 2012 (CEST)
Drachenviereck:
Wenn ein konvexes Viereck zwei Paare gleich langer benachbarter Seiten besitzt, dann nennt man es Drachenviereck. (Konventionaldefinition) --Honeydukes 00:53, 21. Apr. 2012 (CEST)
Ein Drachenviereck ist ein konvexes Viereck, bei dem eine Diagonale auf der Mittelsenkrechten der anderen Diagonalen liegt.
Wenn die Diagonalen eines Viereckes eine Symmetrieachse bildet so spricht man von einem Drachen. --Michael 20:22, 21. Apr. 2012 (CEST)
Diese Definition muss auch noch ein bischen verändert werden... hier einige Vorschläge...
(1) Wenn die Diagonalen eines Viereckes Symmetrieachsen bilden, so spricht man von einem Drachen.
(2) Wenn eine Diagonale eines Viereckes eine Symmetrieachse bildet, so spricht man von einem Drachen.
(3) Wenn die Diagonale eines Viereckes eine Symmetrieachse bildet, so spricht man von einem Drachen.
Vielleicht könnte man an dieser Stelle darüber diskutieren, welche Variante korrekt ist. --Tutor Andreas 18:27, 22. Apr. 2012 (CEST)
Ich würde sagen, dass (2) korrekt ist. Ein Drachendreieck hat zwei Diagonalen, aber nur eine Diagonale bildet die Symmetrieachse. --Honeydukes 22:09, 22. Apr. 2012 (CEST)
Kommentar von m.g.
=Bemerkungen zum Begriff Symmetrieachse
Definition
(Symmetrieachse)
Es sei 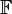 eine beliebige Figur und
eine beliebige Figur und  eine Gerade. Wenn bei der Spiegelung an
eine Gerade. Wenn bei der Spiegelung an 
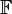 auf sich selbst abgebildet wird, ist
auf sich selbst abgebildet wird, ist  eine Symmetrieachse von
eine Symmetrieachse von 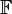
Eine Gerade ist nicht einfach so eine Symmetrieachse, sondern immer eine Symmetrieachse von irgendeinem anderen geometrischen Objekt. A priori ist jede Gerade eine Symmetrieachse: Es sei  eine Gerade in einer Ebene
eine Gerade in einer Ebene  . Ferner sei
. Ferner sei  ein Punkt von
ein Punkt von  . In
. In  existiert jetzt
existiert jetzt 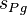 , die Senkrechte in
, die Senkrechte in  auf
auf  . Weil bei der Spiegelung an
. Weil bei der Spiegelung an  die Gerade
die Gerade 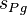 auf sich selbst abgebildet wird, ist
auf sich selbst abgebildet wird, ist  eine Symmetrieachse von
eine Symmetrieachse von 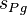 .
.
gleichschenkliges Trapez
Ein Trapez, welches zwei gleichlange Schenkel besitzt, heißt gleichschenkliges Trapez. --Honeydukes 22:22, 22. Apr. 2012 (CEST)
Dann müssen Sie aber auch den Begriff Schenkel eines Trapez definieren. Und könnte zwei Seiten eines Vierecks eigentlich Schenkel sein, wenn sie nicht gleichlang wären?--*m.g.* 17:46, 23. Apr. 2012 (CEST)

