Lösung von Aufgabe 1.3 (SoSe 12): Unterschied zwischen den Versionen
| Zeile 18: | Zeile 18: | ||
Ja, genau diese Formel meine ich. --[[Benutzer:Honeydukes|Honeydukes]] 22:45, 22. Apr. 2012 (CEST)<br /> | Ja, genau diese Formel meine ich. --[[Benutzer:Honeydukes|Honeydukes]] 22:45, 22. Apr. 2012 (CEST)<br /> | ||
| + | |||
| + | Ich war gerade auf dem falschen Weg unterwegs. <math>\left| MP \right|</math> geht ja überhaupt nicht! Es gibt keinen Abstand zwischen einem Punkt und einer Menge- nur zwischen zwei Punkten! Ist das korrekt? Ebenfalls fehlt, dass M und alle Elemente von P in der Ebene liegen. --[[Benutzer:Honeydukes|Honeydukes]] 22:57, 24. Apr. 2012 (CEST) | ||
| Zeile 23: | Zeile 25: | ||
Zu 2.): | Zu 2.): | ||
| − | Die Definition halte ich für fast richtig. Es fehlt meiner Meinung nach die Angabe "für alle X Element P". --[[Benutzer:Honeydukes|Honeydukes]] | + | Die Definition halte ich für fast richtig. Es fehlt meiner Meinung nach die Angabe "für alle X Element P". Ebenfalls weis man nicht, wo der Punkt x und die Punkte der Punktmenge liegen- Es fehlt der Hinweis auf die Ebene. --[[Benutzer:Honeydukes|Honeydukes]] 22:57, 24. Apr. 2012 (CEST) |
| + | |||
| Zeile 30: | Zeile 33: | ||
Verstehe die Formeln nicht. Kann mir jemand sagen was R+ ist? Kann sie jemand formulieren, das würde mir weiterhelfen? --[[Benutzer:Honeydukes|Honeydukes]] 20:43, 21. Apr. 2012 (CEST)<br /> | Verstehe die Formeln nicht. Kann mir jemand sagen was R+ ist? Kann sie jemand formulieren, das würde mir weiterhelfen? --[[Benutzer:Honeydukes|Honeydukes]] 20:43, 21. Apr. 2012 (CEST)<br /> | ||
Unter <math>\mathbb{R}^{+}</math> verstehen wir die Menge aller positiven reellen Zahlen.--[[Benutzer:Schnirch|Schnirch]] 13:42, 23. Apr. 2012 (CEST) | Unter <math>\mathbb{R}^{+}</math> verstehen wir die Menge aller positiven reellen Zahlen.--[[Benutzer:Schnirch|Schnirch]] 13:42, 23. Apr. 2012 (CEST) | ||
| + | |||
| + | Hätte jetzt gesagt, dass die drei richtig ist! Für mich sind die beiden Definitionen bis auf X ∈ E in der 3.) gleich. Das fehlt in der 4.) | ||
| + | --[[Benutzer:Honeydukes|Honeydukes]] 22:57, 24. Apr. 2012 (CEST) | ||
| + | |||
| + | |||
Zu 5.): | Zu 5.): | ||
| − | Ich würde sagen, die Definition ist korrekt. Ein Kreis ist eine geometrische Form in der Ebene (sonst könnte es eine Kugel sein). Bei einem Kreis befindet sich der Mittelpunkt auf gleicher Ebene wie die Punkte der Punktmenge (Jeder Kreis ist eine Menge von Punkten!). Alle diese Punkte der Punktmenge haben bei einem Kreis den gleichen Abstand zum Mittelpunkt (|MP| ist konstant). --[[Benutzer:Honeydukes|Honeydukes]] 20:43, 21. Apr. 2012 (CEST)<br /> | + | Ich würde sagen, die Definition ist nicht korrekt. Ein Kreis ist eine geometrische Form in der Ebene (sonst könnte es eine Kugel sein). Bei einem Kreis befindet sich der Mittelpunkt auf gleicher Ebene wie die Punkte der Punktmenge (Jeder Kreis ist eine Menge von Punkten!). Alle diese Punkte der Punktmenge haben bei einem Kreis den gleichen Abstand zum Mittelpunkt (|MP| ist konstant). --[[Benutzer:Honeydukes|Honeydukes]] 20:43, 21. Apr. 2012 (CEST)<br /> |
| + | Ja, ich habs gerade gemerkt. Hier ist das selbe Problem wir in 1.) zu sehen: Es gibt keinen Abstand zwischen einem Punkt und einer Menge (Punktmenge)! --[[Benutzer:Honeydukes|Honeydukes]] 22:57, 24. Apr. 2012 (CEST) | ||
| + | |||
Die Lösungen der Aufgabe stimmt so noch nicht alle - diskutiert und korrigiert euch selbst!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:57, 24. Apr. 2012 (CEST) | Die Lösungen der Aufgabe stimmt so noch nicht alle - diskutiert und korrigiert euch selbst!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:57, 24. Apr. 2012 (CEST) | ||
Version vom 24. April 2012, 21:57 Uhr
Welche Definition für Kreis ist richtig? Warum (nicht)?
1.) Sei  ein Punkt und P eine Menge, deren Elemente Punkte sind. Wenn gilt:
ein Punkt und P eine Menge, deren Elemente Punkte sind. Wenn gilt:  ist konstant, so ist P ein Kreis mit Mittelpunkt M.
ist konstant, so ist P ein Kreis mit Mittelpunkt M.
2.) Sei M ein Punkt und P eine Punktmenge. Wenn gilt: X∈P∶ |XM|= r, dann ist P ein Kreis.
3.) Sei M ein Punkt in der Ebene E und P eine Punktmenge. Wenn für alle X∈P gilt∶ |XM|= r, r 
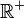 und X ∈ E, dann ist P ein Kreis mit dem Mittelpunkt M.
und X ∈ E, dann ist P ein Kreis mit dem Mittelpunkt M.
4.) Sei M ein Punkt in der Ebene E und P eine Menge, deren Elemente Punkte sind. Wenn für alle X∈P gilt∶ |XM|= r, r
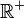 , dann ist P ein Kreis.
, dann ist P ein Kreis.
5.) Sei M ein Punkt und P eine Menge, deren Elemente Punkte sind. Alle Elemente von P liegen in ein und derselben Ebene wie M. Wenn gilt: |MP| ist konstant, so ist P ein Kreis mit Mittelpunkt M.
Zur 1.):
Ich hätte gesagt, dass die Definition falsch ist. Es ist die Rede von Mächtigkeit/ Betrag von MP, aber eigentlich müsste dastehen: Betrag der STRECKE von MP. (Ich wollte eine neue Formel einfügen, habe es aber nicht hinbekommen!) --Honeydukes 20:43, 21. Apr. 2012 (CEST)
Meintest du sowas |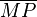 | ?--Tutor Andreas 18:40, 22. Apr. 2012 (CEST)
| ?--Tutor Andreas 18:40, 22. Apr. 2012 (CEST)
Ja, genau diese Formel meine ich. --Honeydukes 22:45, 22. Apr. 2012 (CEST)
Ich war gerade auf dem falschen Weg unterwegs.  geht ja überhaupt nicht! Es gibt keinen Abstand zwischen einem Punkt und einer Menge- nur zwischen zwei Punkten! Ist das korrekt? Ebenfalls fehlt, dass M und alle Elemente von P in der Ebene liegen. --Honeydukes 22:57, 24. Apr. 2012 (CEST)
geht ja überhaupt nicht! Es gibt keinen Abstand zwischen einem Punkt und einer Menge- nur zwischen zwei Punkten! Ist das korrekt? Ebenfalls fehlt, dass M und alle Elemente von P in der Ebene liegen. --Honeydukes 22:57, 24. Apr. 2012 (CEST)
Zu 2.):
Die Definition halte ich für fast richtig. Es fehlt meiner Meinung nach die Angabe "für alle X Element P". Ebenfalls weis man nicht, wo der Punkt x und die Punkte der Punktmenge liegen- Es fehlt der Hinweis auf die Ebene. --Honeydukes 22:57, 24. Apr. 2012 (CEST)
Zu 3. und 4.):
Verstehe die Formeln nicht. Kann mir jemand sagen was R+ ist? Kann sie jemand formulieren, das würde mir weiterhelfen? --Honeydukes 20:43, 21. Apr. 2012 (CEST)
Unterverstehen wir die Menge aller positiven reellen Zahlen.--Schnirch 13:42, 23. Apr. 2012 (CEST)
Hätte jetzt gesagt, dass die drei richtig ist! Für mich sind die beiden Definitionen bis auf X ∈ E in der 3.) gleich. Das fehlt in der 4.) --Honeydukes 22:57, 24. Apr. 2012 (CEST)
Zu 5.):
Ich würde sagen, die Definition ist nicht korrekt. Ein Kreis ist eine geometrische Form in der Ebene (sonst könnte es eine Kugel sein). Bei einem Kreis befindet sich der Mittelpunkt auf gleicher Ebene wie die Punkte der Punktmenge (Jeder Kreis ist eine Menge von Punkten!). Alle diese Punkte der Punktmenge haben bei einem Kreis den gleichen Abstand zum Mittelpunkt (|MP| ist konstant). --Honeydukes 20:43, 21. Apr. 2012 (CEST)
Ja, ich habs gerade gemerkt. Hier ist das selbe Problem wir in 1.) zu sehen: Es gibt keinen Abstand zwischen einem Punkt und einer Menge (Punktmenge)! --Honeydukes 22:57, 24. Apr. 2012 (CEST)
Die Lösungen der Aufgabe stimmt so noch nicht alle - diskutiert und korrigiert euch selbst!--Tutorin Anne 11:57, 24. Apr. 2012 (CEST)

