Lösung von Aufgabe 2.5 (SoSe 12 P): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Wir gehen von folgender Implikation aus: Wenn zwei Geraden g und h nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.<br /> a) Wie lautet die …“) |
|||
| Zeile 2: | Zeile 2: | ||
a) Wie lautet die Kontraposition dieser Implikation?<br /> | a) Wie lautet die Kontraposition dieser Implikation?<br /> | ||
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?<br /> | b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?<br /> | ||
| + | |||
| + | |||
| + | _________________ | ||
| + | |||
| + | |||
| + | a) Beispiel: <math>A \Rightarrow B</math> <br /> | ||
| + | |||
| + | Kontraposition <math>\neg B \Rightarrow \neg A</math> | ||
| + | |||
| + | Geraden keinen (<math>\neg</math>höchstens einen Punkt) Punkt gemeinsam <math>\Rightarrow</math> g <math>\neq</math> h <br /> | ||
| + | |||
| + | b) Behauptung negieren, und dann zum Widerspruch führen: | ||
| + | |||
| + | g <math>\neq </math> h <math>\Rightarrow</math> <math>\neg </math>einen gemeinsamen Punkt<br /> | ||
| + | |||
| + | --[[Benutzer:Honeydukes|Honeydukes]] 00:48, 29. Apr. 2012 (CEST)<br /> | ||
| + | |||
| + | _________________ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
Version vom 28. April 2012, 23:48 Uhr
Wir gehen von folgender Implikation aus: Wenn zwei Geraden g und h nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?
_________________
a) Beispiel: 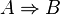
Kontraposition 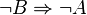
Geraden keinen ( höchstens einen Punkt) Punkt gemeinsam
höchstens einen Punkt) Punkt gemeinsam  g
g  h
h
b) Behauptung negieren, und dann zum Widerspruch führen:
g  h
h 
 einen gemeinsamen Punkt
einen gemeinsamen Punkt
--Honeydukes 00:48, 29. Apr. 2012 (CEST)
_________________

