Diskussion über alternative Lsöung: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „ich habe über deine deine alternative lösung nachgedacht:<br /> A sei die menge der geraden natürlichen zahlen: <math>\ A = \{n\in \mathbb{N} |\exist m\in \mat…“) |
|||
| Zeile 1: | Zeile 1: | ||
| − | ich habe über deine deine alternative lösung nachgedacht:<br /> | + | |
| + | Hier habe ich mir mal eine alternative Lösung überlegt : A { n e N | Em e N : 2m = n } B { n e N | Em e N : (2m)² = n²} | ||
| + | => A = B --[[Benutzer:Bischoffp|Bischoffp]] 13:19, 20. Apr. 2012 (CEST)<br />ich habe über deine deine alternative lösung nachgedacht:<br /> | ||
A sei die menge der geraden natürlichen zahlen: | A sei die menge der geraden natürlichen zahlen: | ||
<math>\ A = \{n\in \mathbb{N} |\exist m\in \mathbb{N}.2m=n\}</math><br />ich hätte für B ne andere lösung:<br /> | <math>\ A = \{n\in \mathbb{N} |\exist m\in \mathbb{N}.2m=n\}</math><br />ich hätte für B ne andere lösung:<br /> | ||
Aktuelle Version vom 29. April 2012, 15:44 Uhr
Hier habe ich mir mal eine alternative Lösung überlegt : A { n e N | Em e N : 2m = n } B { n e N | Em e N : (2m)² = n²}
=> A = B --Bischoffp 13:19, 20. Apr. 2012 (CEST)
ich habe über deine deine alternative lösung nachgedacht:
A sei die menge der geraden natürlichen zahlen:
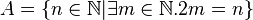
ich hätte für B ne andere lösung:
B sei die menge der natürlichen zahlen, deren quadrate gerade sind:
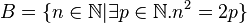
ausserdem glaube ich, dass wir nicht einfach A=B schreiben können.
um zu zeigen, dass A=B, müssten wir zeigen, dass A 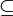 B
B  B
B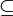 A,
A,
dass also ein beliebiges n, das element von A ist, auch element aus B sein muss.
und dass jedes beliebige n, dass element aus B ist, auch element aus A sein muss,
oder?
--Studentin 01:40, 21. Apr. 2012 (CEST)
Wenn du für deine Menge B z.B. p=3 setzt, dann wäre n meiner Meinung nach keine natürliche Zahl mehr. Wie ich die Äquivalenz hätte anders zeigen sollen , wusste ich nicht :)--Bischoffp 13:16, 21. Apr. 2012 (CEST)
ich will aber gar nicht p=3 setzen, sondern sage, dass in der menge b die zahlen n (aus den natürlichen zahlen) sind, deren quadratzahl gerade sind.
zu deren quadratzahlen also ein p (aus den natürlichen zahlen) existiert, bei dem gilt: n²=2p.
so gehört die 1 nicht zu der menge b: 1²=1 und es gibt kein p aus den natürlichen zahlen, so dass 2p=1
die zahl 2 gehört dazu: 2²=4, das dazu passende p=2
3 dagegen ist nicht element der menge: 3²=9 - dazu existiert kein passendes p
zu 4 dagegen existiert wieder ein p: die quadratzahl zu 4 ist 16, das existierende p lautet 8.
es ist nicht gefordert, dass es zu jedem p aus den natürlichen zahlen ein n geben muss (wie bei deinem bsp. mit der drei), du musst nur ein existierendes p finden, mit der das geforderte wahr wird.
lg--Studentin 21:37, 21. Apr. 2012 (CEST)

