Lösung von Aufgabe 2.4 S (SoSe 12): Unterschied zwischen den Versionen
Zigzag (Diskussion | Beiträge) K (→Aufgabe 2.4) |
|||
| Zeile 13: | Zeile 13: | ||
a) Wenn ein <math>\overline {ABC}</math> zwei kongruente Innenwinkel hat, dann ist dieses Dreieck ein gleichschenkliches Dreieck.<br /> | a) Wenn ein <math>\overline {ABC}</math> zwei kongruente Innenwinkel hat, dann ist dieses Dreieck ein gleichschenkliches Dreieck.<br /> | ||
b) Voraussetzung: <math>\overline {ABC}</math> ist ein Dreieck mit zwei kongruenten Innenwinkeln.<br /> | b) Voraussetzung: <math>\overline {ABC}</math> ist ein Dreieck mit zwei kongruenten Innenwinkeln.<br /> | ||
| − | Behauptung: <math>\overline {ABC}</math> ist ein gleichschenkliges Dreieck. | + | Behauptung: <math>\overline {ABC}</math> ist ein gleichschenkliges Dreieck.[[Benutzer:Zigzag|Zigzag]] |
Version vom 30. April 2012, 06:47 Uhr
Aufgabe 2.4
Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
a) Formulieren Sie den Satz mit "Wenn... dann..."
b) Ergänzen Sie:
Voraussetzung: 
ist ein Dreieck mit…
Behauptung:
a) Wenn ein zwei kongruente Innenwinkel hat, dann ist dieses Dreieck ein gleichschenkliches Dreieck.
b) Voraussetzung: ist ein Dreieck mit zwei kongruenten Innenwinkeln.
Behauptung: ist ein gleichschenkliges Dreieck.Zigzag
b) Vor.: ist ein Dreieck mit 
= 
Beh.: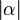 
= 
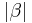--Oz44oz 19:04, 27. Apr. 2012 (CEST)
Ist es bei b) nicht genau andersrum wie bei 0z44oz:
Vorraussetzung :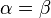 
Behauptung :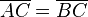
--Funkdocta 15:16, 29. Apr. 2012 (CEST)
- Hier haben wir zwei verschiedene Meinungen und es wäre gut, wenn man an dieser Stelle darüber diskutieren würde.
Es hilft oft, wenn man, wie in Aufgabenteil a) gefordert, den Satz in "Wenn..., dann" formuliert. Man kann dann in dem Satzteil mit "Wenn" die Voraussetzung erkennen und nach dem "dann" kommt die Behauptung. Es lohnt sich daher, dieses "Übersetzen" zu üben.--Tutor Andreas 15:39, 29. Apr. 2012 (CEST)
