Lösung von Aufgabe 5.1P (SoSe 12): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Das Parallelenaxiom lautet wie folgt:<br /> Zu jeder Geraden ''g'' und zu jedem nicht auf ''g'' liegenden Punkt ''A'' gibt es höchstens eine Gerade, die durch '…“) |
|||
| Zeile 7: | Zeile 7: | ||
| + | <math>\ a \|| b \wedge b \|| c \Rightarrow \ a \|| c</math> . <br /> | ||
| + | für den widerspruchsbeweis nehme ich nun <br /> | ||
| + | 1. die behauptung:<math>\ a \|| b \wedge b \|| c </math> <br /> | ||
| + | und <br /> | ||
| + | 2. die annahme (gegenteil der behauptung):<math> a\not \parallel c</math>,<br /> | ||
| + | um sie zu einem widerspruch zu führen.<br /> | ||
| + | |||
| + | [[Datei:Parallele mit schnittpunkt 001.jpg|600px]]<br /> | ||
| + | wenn a und c nicht parallel sind, haben sie einen schnittpunkt.<br /> | ||
| + | es ist gegeben, dass <math>\ a \|| b \wedge b \|| c </math>, beide (a und c) müssen also zu b parallel sein.<br /> | ||
| + | da der schnittpunkt auf beiden liegt und das parallelaxiom gilt, gibt es durch dieses schnittpunkt nur eine (nicht zwei(a und c)) parallele geraden. a und c müssen also identisch sein. | ||
| + | --[[Benutzer:Studentin|Studentin]] 09:35, 11. Mai 2012 (CEST) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 11. Mai 2012, 08:35 Uhr
Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: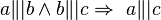 
.
b) Welche Eigenschaft der Relation 
auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
.
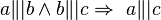für den widerspruchsbeweis nehme ich nun
1. die behauptung: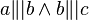
und
2. die annahme (gegenteil der behauptung):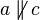
,
um sie zu einem widerspruch zu führen.
wenn a und c nicht parallel sind, haben sie einen schnittpunkt.
es ist gegeben, dass 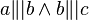, beide (a und c) müssen also zu b parallel sein.
da der schnittpunkt auf beiden liegt und das parallelaxiom gilt, gibt es durch dieses schnittpunkt nur eine (nicht zwei(a und c)) parallele geraden. a und c müssen also identisch sein.
--Studentin 09:35, 11. Mai 2012 (CEST)
