Lösung von Aufgabe 5.1P (SoSe 12): Unterschied zwischen den Versionen
| Zeile 28: | Zeile 28: | ||
!Beweisschritt!!Begründung | !Beweisschritt!!Begründung | ||
|- | |- | ||
| − | | (1) || 1. | + | | (1) a nicht parallel c || 1. somit Schnittpunkt a und c |
|- | |- | ||
| − | | (2) || 2.. | + | | (2) b nicht parallel c || 2. Da Schnittpunkt auf beiden ist |
| − | |} | + | |- |
| + | | (3) a||b und b nicht parallel c || 3. Parallelaxiom | ||
| + | |} | ||
| + | so ?--[[Benutzer:Malilglowka|Malilglowka]] 15:18, 23. Mai 2012 (CEST) | ||
b) Welche Eigenschaft der Relation <math>\|| </math> auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?<br /> | b) Welche Eigenschaft der Relation <math>\|| </math> auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?<br /> | ||
die relation <math>\|| </math> ist transitiv.--[[Benutzer:Studentin|Studentin]] 09:39, 11. Mai 2012 (CEST) | die relation <math>\|| </math> ist transitiv.--[[Benutzer:Studentin|Studentin]] 09:39, 11. Mai 2012 (CEST) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 23. Mai 2012, 14:18 Uhr
Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: 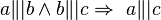 .
.
b) Welche Eigenschaft der Relation  auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: 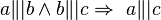 .
.
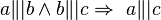 .
.
für den widerspruchsbeweis nehme ich nun
1. die behauptung: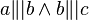
du meinst sicher die Voraussetzung, die du richtig genannt hast.--Tutorin Anne 18:27, 22. Mai 2012 (CEST)
und
2. die annahme (gegenteil der behauptung):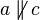 ,
,
um sie zu einem widerspruch zu führen.

wenn a und c nicht parallel sind, haben sie einen schnittpunkt.
es ist gegeben, dass 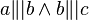 , beide (a und c) müssen also zu b parallel sein.
, beide (a und c) müssen also zu b parallel sein.
da der schnittpunkt auf beiden liegt und das parallelaxiom gilt, gibt es durch dieses schnittpunkt nur eine (nicht zwei(a und c)) parallele geraden. a und c müssen also identisch sein.
--Studentin 09:35, 11. Mai 2012 (CEST)
sehr gut! Natürlich lässt sich das auch in Form einer Tabelle aufführen. Möchten sich noch andere versuchen?--Tutorin Anne 18:27, 22. Mai 2012 (CEST)
In dem Sinne ist der Widerspruch widerlegt da in dem Fall a und c einen Schnittpunkt haben und da durch das Axiom kein Punkt A auf der geraden a liegen darf ist nur b mit a parallel aber nicht b mit c und somit ist auch nicht a mit c. habe cih das richtig verstanden? --Malilglowka 15:12, 23. Mai 2012 (CEST)
durch den punkt a darf nur eine(!) gerade geben, die zur geraden b parallel ist (p.-axiom), da a und c durch den schnittpunkt gehen, müssen beide identisch sein.--Studentin 15:17, 23. Mai 2012 (CEST)
| Beweisschritt | Begründung | |
|---|---|---|
| (1) a nicht parallel c | 1. somit Schnittpunkt a und c | |
| (2) b nicht parallel c | 2. Da Schnittpunkt auf beiden ist | |
| (3) a | b und b nicht parallel c | 3. Parallelaxiom |
so ?--Malilglowka 15:18, 23. Mai 2012 (CEST)
b) Welche Eigenschaft der Relation  auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
die relation  ist transitiv.--Studentin 09:39, 11. Mai 2012 (CEST)
ist transitiv.--Studentin 09:39, 11. Mai 2012 (CEST)

