Lösung von Aufg. 5.3P (SoSe 12): Unterschied zwischen den Versionen

Version vom 25. Mai 2012, 11:26 Uhr

Definition: Halbgerade $AB^-$

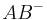Gegeben seien zwei nicht identische Punkte $\ A$ und $\ B$ . Unter $\ AB^-$ wollen wir die Menge aller Punkte $\ P$ verstehen, die man erhält, wenn man $\overline{AB}$ über $\ A$ hinaus verlängert.

Geben Sie eine formal korrekte Definition für die Menge dieser Punkte $\ P$ an.

$AB^-$ = {P} \ $AB^+$

Damit meien ich alle Punkte P die nicht auf $AB^+$ liegen somit ist ja schon alles ausgeschlossen und es ist $AB^-$ definiert? oder? --Malilglowka 15:51, 23. Mai 2012 (CEST)

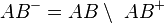du meinst bestimmt $\ AB^{-} = AB \setminus \ AB^{+}$ ,
also die gesamte gerade, die durch a und b geht, aber ohne $\ AB^{+}$ , oder?

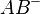zu $\ AB^{+}$ und $\ AB^{-}$ gehört jeweils der punkt a.
wenn du also $\ AB^{+}$ von der geraden abziehst, fehlt der halbgeraden das der punkt a, daher muss dieser noch zugefügt werden:
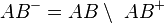
$\ AB^{-} = AB \setminus \ AB^{+}$ $\cup \{ A\}$
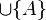
--Studentin 16:13, 23. Mai 2012 (CEST)

Ich verstehe die Def. nicht ganz. Warum genügt es bei AB^- {P| ZW(P,A,B)} U {A} zu schreiben? Ich weiß, dass damit gesagt wird, dass NUR die Strecke |PA| OHNE |AB| + A zu bedrachten ist. Bei AB^+ schreiben wir jedoch |AB| U {P| ZW(A,B,P)} und beziehen bei der ZW hierbei |BP| mit ein (der rechte Teil der Halbstrecke, der nach |AB| kommt). Ich glaube mein Problem bezieht sich auf das Verständnis der ZW. Bei AB^+ schreiben wir ZW(A,B,P) und meinen die Strecke |AB|+|BP|?! Bei AB^- schreiben wir ZW(P,A,B) und meinen |PA| OHNE |AB|?! Das erscheint mir etwas unverständlich, bitte um Hilfe! Schnitzel

@@ Zeile 19: / Zeile 19: @@
 --[[Benutzer:Studentin|Studentin]] 16:13, 23. Mai 2012 (CEST)
 -------------------------------------------------------------------------------------------------------
-Ich verstehe die Def. nicht ganz. Warum genügt es bei AB^- {P| ZW(P,A,B)} U {A} zu schreiben? Ich weiß, dass damit gesagt wird, dass NUR die Strecke |PA| OHNE |PB| + A zu bedrachten ist.
+Ich verstehe die Def. nicht ganz. Warum genügt es bei AB^- {P| ZW(P,A,B)} U {A} zu schreiben? Ich weiß, dass damit gesagt wird, dass NUR die Strecke |PA| OHNE |AB| + A zu bedrachten ist.
 Bei AB^+ schreiben wir '''jedoch'''  |AB| U {P| ZW(A,B,P)}  und beziehen bei der ZW hierbei |BP| mit ein (der rechte Teil der Halbstrecke, der nach |AB| kommt).
 Ich glaube mein Problem bezieht sich auf das Verständnis der ZW. Bei AB^+ schreiben wir ZW(A,B,P) und meinen die Strecke |AB|+|BP|?! Bei AB^- schreiben wir ZW(P,A,B) und meinen |PA| OHNE |AB|?! Das erscheint mir etwas unverständlich, bitte um Hilfe!  [[Benutzer:Schnitzel|Schnitzel]]
 [[Kategorie:Einführung_P]]

Lösung von Aufg. 5.3P (SoSe 12): Unterschied zwischen den Versionen

Version vom 25. Mai 2012, 11:26 Uhr

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Werkzeuge