Lösung von Aufg. 5.3P (SoSe 12)

Definition: Halbgerade $AB^-$

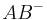Gegeben seien zwei nicht identische Punkte $\ A$ und $\ B$. Unter $\ AB^-$ wollen wir die Menge aller Punkte $\ P$ verstehen, die man erhält, wenn man $\overline{AB}$ über $\ A$ hinaus verlängert.

Geben Sie eine formal korrekte Definition für die Menge dieser Punkte $\ P$ an.

$AB^-$ = {P} \ $AB^+$

Damit meien ich alle Punkte P die nicht auf $AB^+$ liegen somit ist ja schon alles ausgeschlossen und es ist $AB^-$ definiert? oder? --Malilglowka 15:51, 23. Mai 2012 (CEST)

du meinst bestimmt $\ AB^{-} = AB \setminus \ AB^{+}$ ,
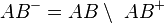also die gesamte gerade, die durch a und b geht, aber ohne $\ AB^{+}$ , oder?

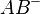zu $\ AB^{+}$ und $\ AB^{-}$ gehört jeweils der punkt a.
wenn du also $\ AB^{+}$ von der geraden abziehst, fehlt der halbgeraden das der punkt a, daher muss dieser noch zugefügt werden:
$\ AB^{-} = AB \setminus \ AB^{+}$ $\cup \{ A\}$
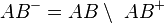
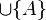
--Studentin 16:13, 23. Mai 2012 (CEST)

---

Ich verstehe die Def. nicht ganz. Warum genügt es bei AB^- {P| ZW(P,A,B)} U {A} zu schreiben? Ich weiß, dass damit gesagt wird, dass NUR die Strecke |PA| OHNE |AB| + A zu bedrachten ist.

Bei AB^+ schreiben wir jedoch |AB| U {P| ZW(A,B,P)} und beziehen bei der ZW hierbei |BP| mit ein (der rechte Teil der Halbstrecke, der nach |AB| kommt). Ich glaube mein Problem bezieht sich auf das Verständnis der ZW. Bei AB^+ schreiben wir ZW(A,B,P) und meinen die Strecke |AB|+|BP|?! Bei AB^- schreiben wir ZW(P,A,B) und meinen |PA| OHNE |AB|?! Das erscheint mir etwas unverständlich, bitte um Hilfe! Schnitzel

eine orangene geschweifte klammer hab ich vergessen zu schreiben...--Studentin 15:59, 25. Mai 2012 (CEST)
hallo
leider vertehe ich deine frage nicht ganz, da es nie um eine strecke |ap| geht.
bei ab+ geht es um die halbgerade, die bei a beginnt, und zwar ins unendliche in richtung b
bei ab+ geht es um die halbgerade, die bei a beginnt, und zwar ins unendliche in richtung entgegengesetzt b
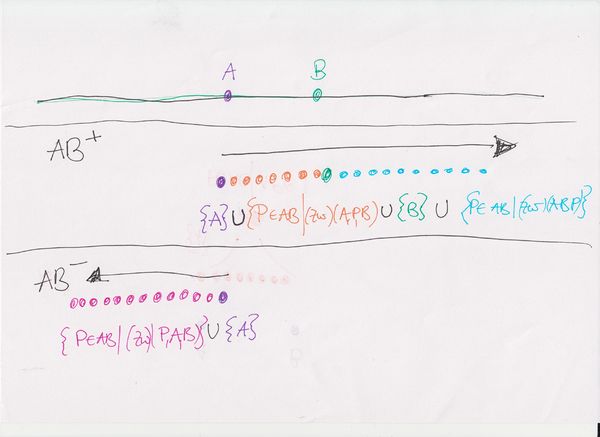
im beispiel in der zeichnung also:
ab+: alle punkte, die links von a liegen, einschließlich a
ab-: alle punkte, die rechts von a liegen einschließlich a

aufgedröselt wäre es für ab+:
orange: alle punkte p zw. a und b
türkis: alle punkte p rechts von b
lila: punkt a
grün: punkt b

aufgedröselt wäre es für ab-:
pink: alle punkte p links von a
lila: punkt a

oben steht noch ein anderer vorschlag:
man nimmt, um ab- zu erhalten, die gesamte gerade (in der zeichnung ganz oben im bild),
zieht von dieser ab+ ab (also alles rechts von a (einschließlich a)) und muss dann aber a nochmals dazugeben
(da a ja mit ab+ abgezogen wurde.)--Studentin 15:59, 25. Mai 2012 (CEST)

p.s.: vielleicht hast du dieses problem mit zwischen?!?:
wenn zw (a, b, p) geschrieben wird, werden alle punkte gemeint, die in meiner zeichnung rechts von b liegen, die strecke ab ist also nicht dabei (türkis)
wenn zw (p, a, b) geschrieben wird, werden alle punkte gemeint, die in meiner zeichnung links von a liegen, die strecke ab ist also auch nicht dabei (pink).
bei ab+ benötigen wir aber die strecke ab, da wir ja alle punkte brauchen, die rechts von a liegen (also auch die strecke ab), bei ab- benötigen wir die strecke ab dagegen nicht, da sie nicht links von a liegt.
war das die frage?--Studentin 16:06, 25. Mai 2012 (CEST)

Hi Studentin, erstmal vielen Dank für Deine Mühe! Dein zweiter Beitrag erklärt meine Frage und beantwortet diese auch! Eine abschließende Frage - zur Kontrolle, ob ich es wirklich verstanden habe - hätte ich dazu noch. OHNE die Kenntnis der Streckeneinteilung (Bei uns durch AB gegeben) wüsste man aber dann doch nicht, welche Punkte gemeint sind, wenn zum Beispiel zw (a, b, p) gilt, oder? Statt alle Punkte rechts von b, könnten dann doch auch alle Punkte links von b gemeint sein?!

D.h. will man Halbgeraden mit Hilfe von Zwischenrelationen definieren, so muss zuerst die Streckeneinteilung durch zwei Punkte eindeutig festgelegt werden (Bsp. AB). Erst danach gilt für:

1. ZW(A,B,P) = meint alle Punkte, die rechts von B liegen

2. ZW(P,A,B) = meint alle Punkte, die links von A liegen

Eine bloße Zwischenrelation (A,B,C) sagt nur aus, dass B zwischen den beiden Punkten A und C liegt, |AB|+BC|=|AC| gilt und dass der Punkt B sowohl von A als auch von C verschieden ist.

Ich hoffe, dass damit alles geklärt ist und wünsche ein schönes Wochenende :) -----Schnitzel 17:20, 25. Mai 2012 (CEST)

bin mir wieder nicht ganz sicher, was du meinst, aaaaber: so ein "links" oder "rechts" gibt es ja nicht in wirklichkeit.
wenn du dein blatt um 180° drehen würdest, läge b rechts und a links.
drehst du es um 90°, liegt b oben, a unten... :-)

durch zw(a,b,p) ist jedoch festgelegt, dass alle punkte p "seitlich neben" b liegen, und zwar auf der seite, die a abgewandt ist - nur auf meiner zeichnung ist dies "rechts" von b (solange du denn bildschirm auf den kopf stellst ;-))
durch zw(p,a,b) ist festgelegt, dass alle punkte p "seitlich neben" a liegen, und zwar auf der seite, die b abgewandt ist - auf meiner zeichnung ist dies "links" von a
durch zw(a,p,b)) ist festgelegt, dass alle punkte p zwischen a und b liegen.
dir auch ein schönes wochenende --Studentin 20:15, 25. Mai 2012 (CEST)

• Einfach spitzenmäßig! Danke für's Diskutieren - das bringt viele weiter! --Tutorin Anne 19:48, 27. Mai 2012 (CEST)

ich kann mich Tutorin Anne nur anschließen, eine super Diskussion - machen sie weiter so--Schnirch 11:23, 29. Mai 2012 (CEST)