Lösung von Aufg. 5.3P (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 21: Zeile 21:
 
Ich verstehe die Def. nicht ganz. Warum genügt es bei AB^- {P| ZW(P,A,B)} U {A} zu schreiben? Ich weiß, dass damit gesagt wird, dass NUR die Strecke |PA| OHNE |AB| + A zu bedrachten ist.
 
Ich verstehe die Def. nicht ganz. Warum genügt es bei AB^- {P| ZW(P,A,B)} U {A} zu schreiben? Ich weiß, dass damit gesagt wird, dass NUR die Strecke |PA| OHNE |AB| + A zu bedrachten ist.
 
Bei AB^+ schreiben wir '''jedoch'''  |AB| U {P| ZW(A,B,P)}  und beziehen bei der ZW hierbei |BP| mit ein (der rechte Teil der Halbstrecke, der nach |AB| kommt).
 
Bei AB^+ schreiben wir '''jedoch'''  |AB| U {P| ZW(A,B,P)}  und beziehen bei der ZW hierbei |BP| mit ein (der rechte Teil der Halbstrecke, der nach |AB| kommt).
−
Ich glaube mein Problem bezieht sich auf das Verständnis der ZW. Bei AB^+ schreiben wir ZW(A,B,P) und meinen die Strecke |AB|+|BP|?! Bei AB^- schreiben wir ZW(P,A,B) und meinen |PA| OHNE |AB|?! Das erscheint mir etwas unverständlich, bitte um Hilfe!  [[Benutzer:Schnitzel|Schnitzel]]
+
Ich glaube mein Problem bezieht sich auf das Verständnis der ZW. Bei AB^+ schreiben wir ZW(A,B,P) und meinen die Strecke |AB|+|BP|?! Bei AB^- schreiben wir ZW(P,A,B) und meinen |PA| OHNE |AB|?! Das erscheint mir etwas unverständlich, bitte um Hilfe!  [[Benutzer:Schnitzel|Schnitzel]]<br /><br />
 +
 
 +
 
 +
[[Datei:Ab+, ab- 002.jpg|600px]]eine orangene geschweifte klammer hab ich vergessen zu schreiben...--[[Benutzer:Studentin|Studentin]] 15:59, 25. Mai 2012 (CEST)
 +
<br />hallo<br />
 +
leider vertehe ich deine frage nicht ganz, da es nie um eine strecke |ap| geht.<br />
 +
bei ab+ geht es um die halbgerade, die bei a beginnt, und zwar ins unendliche in richtung b <br />
 +
bei ab+ geht es um die halbgerade, die bei a beginnt, und zwar ins unendliche in richtung entgegengesetzt b<br />
 +
im beispiel in der zeichnung also:<br />
 +
ab+: alle punkte, die links von a liegen, einschließlich a<br />
 +
ab-: alle punkte, die rechts von a liegen einschließlich a<br /><br />
 +
aufgedröselt wäre es für ab+: <br />
 +
orange: alle punkte p zw. a und b<br />
 +
türkis: alle punkte p rechts von b<br />
 +
lila: punkt a<br />
 +
grün: punkt b<br /><br />
 +
aufgedröselt wäre es für ab-: <br />
 +
pink: alle punkte p links von a <br />
 +
lila: punkt a<br />
 +
 
 +
oben steht noch ein anderer vorschlag: <br />
 +
man nimmt, um ab- zu erhalten, die gesamte gerade (in der zeichnung ganz oben im bild),<br />
 +
zieht von dieser ab+ ab (also alles rechts von a (einschließlich a)) und muss dann aber a nochmals dazugeben<br />
 +
(da a ja mit ab+ abgezogen wurde.)--[[Benutzer:Studentin|Studentin]] 15:59, 25. Mai 2012 (CEST)
 
[[Kategorie:Einführung_P]]
 
[[Kategorie:Einführung_P]]

Version vom 25. Mai 2012, 14:59 Uhr

Definition: Halbgerade AB^-

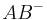Gegeben seien zwei nicht identische Punkte \ A und \ B. Unter \ AB^- wollen wir die Menge aller Punkte \ P verstehen, die man erhält, wenn man \overline{AB} über \ A hinaus verlängert.

Geben Sie eine formal korrekte Definition für die Menge dieser Punkte \ P an.



AB^- = {P} \ AB^+

Damit meien ich alle Punkte P die nicht auf AB^+ liegen somit ist ja schon alles ausgeschlossen und es ist AB^- definiert? oder? --Malilglowka 15:51, 23. Mai 2012 (CEST)

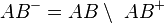du meinst bestimmt \ AB^{-} = AB \setminus \ AB^{+} ,
also die gesamte gerade, die durch a und b geht, aber ohne \ AB^{+} , oder?

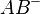zu \ AB^{+} und \ AB^{-} gehört jeweils der punkt a.
wenn du also \ AB^{+} von der geraden abziehst, fehlt der halbgeraden das der punkt a, daher muss dieser noch zugefügt werden:
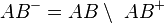
\ AB^{-} = AB \setminus \ AB^{+} \cup \{ A\}
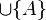
--Studentin 16:13, 23. Mai 2012 (CEST)

Ich verstehe die Def. nicht ganz. Warum genügt es bei AB^- {P| ZW(P,A,B)} U {A} zu schreiben? Ich weiß, dass damit gesagt wird, dass NUR die Strecke |PA| OHNE |AB| + A zu bedrachten ist. Bei AB^+ schreiben wir jedoch |AB| U {P| ZW(A,B,P)} und beziehen bei der ZW hierbei |BP| mit ein (der rechte Teil der Halbstrecke, der nach |AB| kommt). Ich glaube mein Problem bezieht sich auf das Verständnis der ZW. Bei AB^+ schreiben wir ZW(A,B,P) und meinen die Strecke |AB|+|BP|?! Bei AB^- schreiben wir ZW(P,A,B) und meinen |PA| OHNE |AB|?! Das erscheint mir etwas unverständlich, bitte um Hilfe! Schnitzel


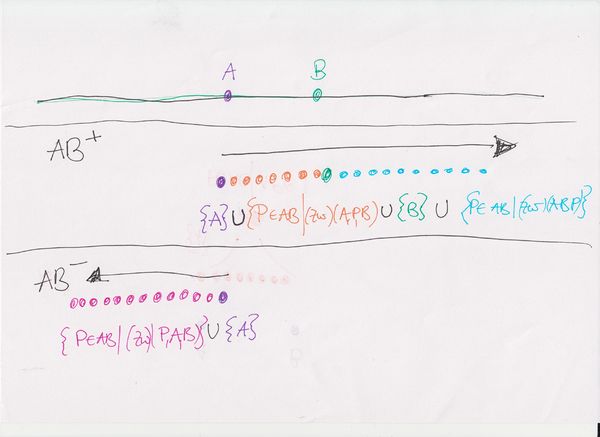Ab+, ab- 002.jpgeine orangene geschweifte klammer hab ich vergessen zu schreiben...--Studentin 15:59, 25. Mai 2012 (CEST)
hallo
leider vertehe ich deine frage nicht ganz, da es nie um eine strecke |ap| geht.
bei ab+ geht es um die halbgerade, die bei a beginnt, und zwar ins unendliche in richtung b
bei ab+ geht es um die halbgerade, die bei a beginnt, und zwar ins unendliche in richtung entgegengesetzt b
im beispiel in der zeichnung also:
ab+: alle punkte, die links von a liegen, einschließlich a
ab-: alle punkte, die rechts von a liegen einschließlich a

aufgedröselt wäre es für ab+:
orange: alle punkte p zw. a und b
türkis: alle punkte p rechts von b
lila: punkt a
grün: punkt b

aufgedröselt wäre es für ab-:
pink: alle punkte p links von a
lila: punkt a

oben steht noch ein anderer vorschlag:
man nimmt, um ab- zu erhalten, die gesamte gerade (in der zeichnung ganz oben im bild),
zieht von dieser ab+ ab (also alles rechts von a (einschließlich a)) und muss dann aber a nochmals dazugeben
(da a ja mit ab+ abgezogen wurde.)--Studentin 15:59, 25. Mai 2012 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._5.3P_(SoSe_12)&oldid=13889“