Übung 9 SoSe 12: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| + | == Aufgabe 9.1 == | ||
| + | Definieren Sie den Begriff ''Inneres eines Dreiecks''.<br /> | ||
| + | [[Lösung von Aufgabe 9.1_S]] | ||
| + | <br /> | ||
| + | |||
| + | |||
| + | == Aufgabe 9.1 == | ||
| + | Definieren Sie die Begriffe ''Stufenwinkel'' und ''Wechselwinkel''.<br /> | ||
| + | [[Lösung von Aufgabe 9.1_S]] | ||
| + | <br /> | ||
| + | |||
| + | |||
== Aufgabe 9.1 == | == Aufgabe 9.1 == | ||
'''Satz:'''<br /> | '''Satz:'''<br /> | ||
Version vom 14. Juni 2012, 13:14 Uhr
Inhaltsverzeichnis |
Aufgabe 9.1
Definieren Sie den Begriff Inneres eines Dreiecks.
Lösung von Aufgabe 9.1_S
Aufgabe 9.1
Definieren Sie die Begriffe Stufenwinkel und Wechselwinkel.
Lösung von Aufgabe 9.1_S
Aufgabe 9.1
Satz:
Jeder rechte Winkel hat das Maß 90.
a) Formulieren Sie mit "wenn...dann..."
b) Beweisen Sie den Satz.
Lösung von Aufgabe 9.1_S
Aufgabe 9.1
Satz:
Es sei  eine Gerade der Ebene
eine Gerade der Ebene  . Ferner sei
. Ferner sei  ein Punkt auf
ein Punkt auf  . In der Ebene
. In der Ebene  gibt es genau eine Gerade
gibt es genau eine Gerade  , die durch
, die durch  geht und senkrecht auf
geht und senkrecht auf  steht.
steht.
Beweisen Sie den Satz.
Lösung von Aufgabe 9.1_S
Aufgabe 9.1
Warum ist die folgende Definition des Begriffs Winkelhalbierende nicht korrekt?
Die Halbgerade 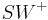 ist die Winkelhalbierende des Winkels
ist die Winkelhalbierende des Winkels  , wenn
, wenn 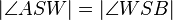 .
.
Eine Skizze genügt.
Lösung von Aufgabe 9.1_S
Aufgabe 9.1
Satz:
Es sei 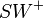 die Winkelhalbierende des Winkels
die Winkelhalbierende des Winkels  . Dann gilt:
. Dann gilt:
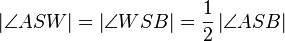
Beweisen Sie den Satz.
Lösung von Aufgabe 9.1_S

