Lösung von Zusatzaufgabe 6.3 S (SoSe 12): Unterschied zwischen den Versionen
K (→Zusatzaufgabe 6.3) |
K (→Zusatzaufgabe 6.3) |
||
| Zeile 26: | Zeile 26: | ||
<br /> | <br /> | ||
Hmmm, ich habe mir überlegt, dass bei dieser Definition (windschief auf der Menge aller Geraden) 3 Eigenschaften ausgeschlossen sein müssen:<br /> | Hmmm, ich habe mir überlegt, dass bei dieser Definition (windschief auf der Menge aller Geraden) 3 Eigenschaften ausgeschlossen sein müssen:<br /> | ||
| − | # Identität | + | # Identität (g<math>\equiv</math> h) |
| − | # Parallelität | + | # Parallelität (<math>g || h</math>) |
# Schnittpunkt ( <math>g \cap h</math>)<br /> | # Schnittpunkt ( <math>g \cap h</math>)<br /> | ||
In deiner 2ten Definition hast Du jetzt durch das "genau einen Punkt gemeinsam" die Identität g=h ausgeschlossen.<br /> | In deiner 2ten Definition hast Du jetzt durch das "genau einen Punkt gemeinsam" die Identität g=h ausgeschlossen.<br /> | ||
Version vom 15. Juni 2012, 17:34 Uhr
Zusatzaufgabe 6.3
a) Definieren Sie windschief auf der Menge aller Geraden (d.h.im Raum) auf zwei verschiedene Arten.
b) Warum ist die folgende Definition sinnlos?
- Zwei Ebenen sind windschief, wenn sie sich nicht schneiden und sie nicht parallel zueinander sind.
- Zwei Ebenen sind windschief, wenn sie sich nicht schneiden und sie nicht parallel zueinander sind.
Lösungsversuch 1
a)
1) Wenn zwei verschiedene Geraden g und h weder parallel sind, noch einen gemeinsamen Schnittpunkt besitzen, dann sind sie windschief.
2) Wenn eine Gerade g in einer Ebene E liegt und eine Gerade h diese Ebene E an einem Punkt schneidet, der nicht zu g gehört, dann sind g und h windschief zueinander.
b) Ebenen sind entweder parallel zueinander oder sie schneiden sich.
--Thommy 20:50, 14. Jun. 2012 (CEST)
I
Ich würde bei 2) noch hinzufügen, dass die Gerade h (wie bei 1) ) auch nicht parallel oder identisch zur Geraden g sein darf..
--Tchu Tcha Tcha 22:06, 14. Jun. 2012 (CEST)
Nach Kommentar von Tchu Tcha Tcha:
2) Wenn eine Gerade g in einer Ebene E liegt und eine Gerade h mit dieser Ebene E "genau" einen Punkt gemeinsam hat, der nicht zu g gehört, dann sind g und h windschief zueinander.
Habe ich die die Möglichkeit von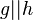 
nicht dadurch ausgeschlossen, dass g in E liegt, h aber nicht in E liegt bzw. h die Ebene E in genau einem Punkt schneiden muss? Aber deine Anmerkung hat trotzdem zu einer kleinen Abänderung geführt. Dankeschön!
--Thommy 16:12, 15. Jun. 2012 (CEST)
Hmmm, ich habe mir überlegt, dass bei dieser Definition (windschief auf der Menge aller Geraden) 3 Eigenschaften ausgeschlossen sein müssen:
- Identität (g
h)
- Parallelität ()
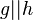- Schnittpunkt (
)
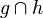In deiner 2ten Definition hast Du jetzt durch das "genau einen Punkt gemeinsam" die Identität g=h ausgeschlossen.
Außerdem glaube ich auch, dass die Gerade h die Ebene E in einem Punkt schneiden muss, wenn sie nicht parallel zur Ebene ist.
Schnittpunkt mit g ist auch ausgeschlossen ("..der nicht zu g gehört..")..
Hoffe Du hast recht und die Lösung/Definition passt so ;-)
--Tchu Tcha Tcha 18:20, 15. Jun. 2012 (CEST)
