Zusatzaufgaben 8 S (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „== Zusatzaufgabe 8.1 == Unter dem Raum <math>\mathbb{P}</math>versteht man die Menge aller Punkte. Die Punktmenge <math>\varepsilon \subset \mathbb{P}</math> sei…“)
 
(→‎Zusatzaufgabe 8.3)
Zeile 14: Zeile 14:
 
[[Lösung von Zusatzaufgabe 8.3_S]]
 
[[Lösung von Zusatzaufgabe 8.3_S]]
 
<br />
 
<br />
 +
 +
z.z. offene HE sind konvexe Punktmengen
 +
Vor: offene HE  gP<sup>+</sup>
 +
Beh: gP<sup>+</sup>
 +
 +
direkter Beweis:
 +
 +
(1) Q sei ein beliebiger weiterer Pkt, der mit P in der offenen Halbebene gP<sup>+</sup> liegt
 +
 +
(2) Es gilt dann: Strecke QP geschnitten mit g = {}; Begründung: Def. Halbebene
 +
 +
(3) dann muss folglich für die Punktmenge R Element der Strecke QP gelten, dass diese mit g geschnitten auch = {}; Begründung: (2)
 +
 +
(4) Alle Punkte auf der Strecke QP gehören zur offenen Halbebene gP<sup>+</sup>; Begründung: (3)
 +
 +
(5) gP<sup>+</sup> ist konvex; Begrüundung: (4)
 +
 +
q.e.d.
 +
 +
Es müssten jedoch noch weitere 2 Fälle betrachtet werden:
 +
 +
1. Dass die 2 Punkte A und B der Punktmenge auf der Trägergerade g liegen
 +
-> Strecke AB liegt vollständig in g und gehört somit auch zur HE gP<sup>+</sup>.
 +
 +
2. Dass ein Punkt A auf der Trägergeraden g liegt und ein Punkt B jedoch in der offenen HE gP<sup>+</sup> liegt.
 +
-> Hierzu teilen wir die Strecke AB in die Strecke AB ohne A und dem Punkt A auf.
 +
Die Strecke AB ohne A hat keinen Schnittpunkt mit g und A gehört zu g und somit auch zur HE gP<sup>+</sup>--[[Benutzer:Sissy66|Sissy66]] 00:09, 18. Jun. 2012 (CEST)
  
 
== Zusatzaufgabe 8.4 ==
 
== Zusatzaufgabe 8.4 ==

Version vom 18. Juni 2012, 00:09 Uhr

Inhaltsverzeichnis

 [Verbergen] 

Zusatzaufgabe 8.1

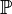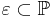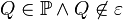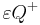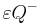Unter dem Raum \mathbb{P}versteht man die Menge aller Punkte. Die Punktmenge \varepsilon \subset \mathbb{P} sei eine Ebene. Gegeben sei ferner \ Q mit Q \in \mathbb{P} \wedge Q \not \in \varepsilon. Definieren Sie die Begriffe Halbraum \varepsilon Q^+ und \varepsilon Q^-.
Lösung von Zusatzaufgabe 8.1_S

Zusatzaufgabe 8.2

Definieren Sie den Begriff Inneres eines Kreises. (Kreis sei bereits definiert.)
Lösung von Zusatzaufgabe 8.2_S

Zusatzaufgabe 8.3

Beweisen Sie: Halbebenen sind konvexe Punktmengen.
Lösung von Zusatzaufgabe 8.3_S

z.z. offene HE sind konvexe Punktmengen Vor: offene HE gP+ Beh: gP+

direkter Beweis:

(1) Q sei ein beliebiger weiterer Pkt, der mit P in der offenen Halbebene gP+ liegt

(2) Es gilt dann: Strecke QP geschnitten mit g = {}; Begründung: Def. Halbebene

(3) dann muss folglich für die Punktmenge R Element der Strecke QP gelten, dass diese mit g geschnitten auch = {}; Begründung: (2)

(4) Alle Punkte auf der Strecke QP gehören zur offenen Halbebene gP+; Begründung: (3)

(5) gP+ ist konvex; Begrüundung: (4)

q.e.d.

Es müssten jedoch noch weitere 2 Fälle betrachtet werden:

1. Dass die 2 Punkte A und B der Punktmenge auf der Trägergerade g liegen -> Strecke AB liegt vollständig in g und gehört somit auch zur HE gP+.

2. Dass ein Punkt A auf der Trägergeraden g liegt und ein Punkt B jedoch in der offenen HE gP+ liegt. -> Hierzu teilen wir die Strecke AB in die Strecke AB ohne A und dem Punkt A auf. Die Strecke AB ohne A hat keinen Schnittpunkt mit g und A gehört zu g und somit auch zur HE gP+--Sissy66 00:09, 18. Jun. 2012 (CEST)

Zusatzaufgabe 8.4

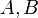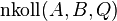Seien A, B und Q drei paarweise verschiedene Punkte für die gelte \operatorname{nkoll}(A, B, Q). Sei g eine Gerade. Beweisen Sie:
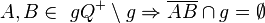A, B \in \ gQ^{+} \setminus g \Rightarrow \overline{AB} \cap g = \emptyset.
Lösung von Zusatzaufgabe 8.4_S

Von „http://geometrie.zum.de/index.php?title=Zusatzaufgaben_8_S_(SoSe_12)&oldid=14993“