Lösung von Aufgabe 7.5 S (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Nemo81 (Diskussion | Beiträge) |
|||
| Zeile 3: | Zeile 3: | ||
| − | Vor: koll(A,B,C) und A,B,C | + | Vor: koll(A,B,C) und A,B,C <math>\not \in </math>g, <math>\overline {AB}</math> <math>\cap</math> g <math>\neq</math> <math>\empty</math> und <math>\overline {BC}\ \cap\ g = \empty</math> |
| − | Beh: | + | Beh: <math>\overline {AC}\ \cap \ g\ \neq\ \empty</math> |
Bew: | Bew: | ||
| − | 1. koll(A,B,C) und A,B,C | + | 1. koll(A,B,C) und A,B,C <math>\not\in</math> g laut Vor: |
| − | 2. AB+BC=AC laut Ax II/3 Dreiecks ungl. | + | 2. |AB| + |BC| = |AC| laut Ax II/3 Dreiecks ungl. |
| + | *Dieser Schritt stimmt so nicht, da eine der drei Gleichungen gelten kann und nicht genau diese. Hier muss man die Fälle unterscheiden.--[[Benutzer:Andreas|Tutor Andreas]] 17:04, 21. Jun. 2012 (CEST) | ||
| − | 3. | + | 3. <math>\overline {AB} \cap g = \{S\}</math> laut Vor. |
| − | 4. | + | 4. Zw(A,S,B) laut 3. und trivial |
| − | 5. AS+SB=AB laut Ax II/3 und 4 | + | 5. |AS| + |SB| = |AB| laut Ax II/3 und 4 |
| − | 6. AS+SB+BC=AC laut Rechnen in R, 5. und 2. | + | 6. |AS| + |SB| + |BC| = |AC| laut Rechnen in R, 5. und 2. |
| − | 7. AS+SC=AC laut Rechnen in R und 6. | + | 7. |AS| + |SC| = |AC| laut Rechnen in R und 6. |
8. Zw(A,S,C) laut 7 und Ax II/3 | 8. Zw(A,S,C) laut 7 und Ax II/3 | ||
| − | 9. Unmittelbar folgt | + | 9. Unmittelbar folgt <math>\overline {AC}\ \cap \ g\ \neq\ \empty</math> weil <math>\overline {AC}\ \cap \ g\ =\ \{S\}</math> laut 8. und trivial q.e.d --[[Benutzer:Nemo81|Nemo81]] 18:55, 14. Jun. 2012 (CEST) |
Version vom 21. Juni 2012, 16:04 Uhr
 --KeinKurpfälzer 17:29, 11. Jun. 2012 (CEST) Idee von Wurzel
--KeinKurpfälzer 17:29, 11. Jun. 2012 (CEST) Idee von Wurzel
--Tchu Tcha Tcha 19:14, 12. Jun. 2012 (CEST)
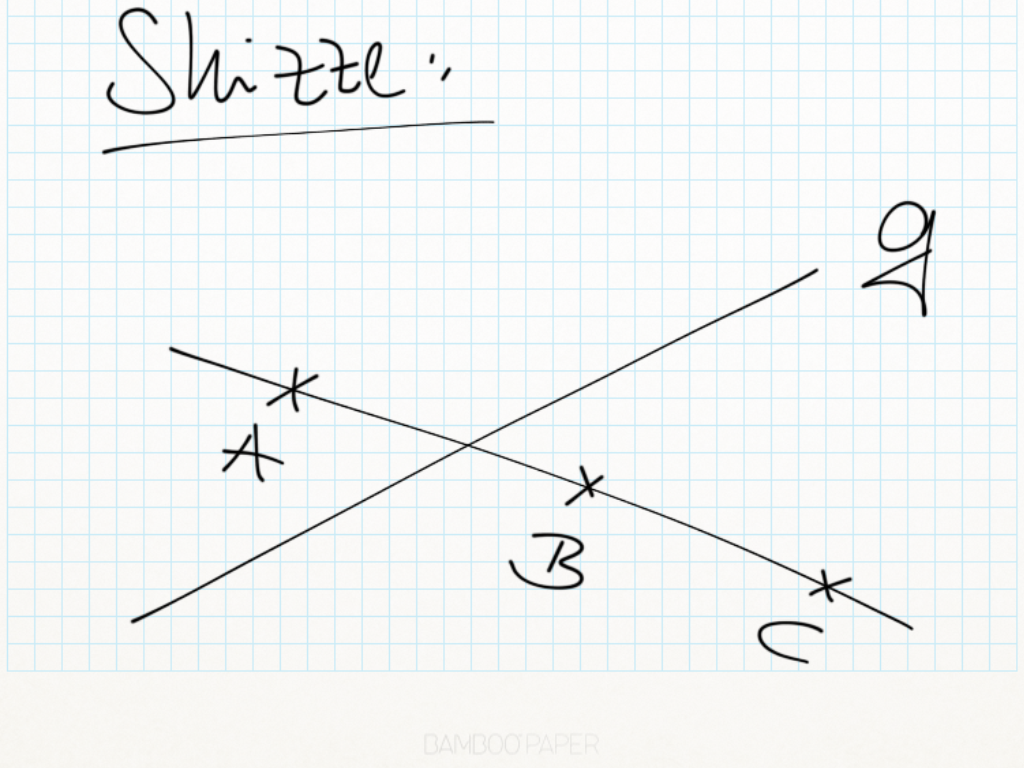
Vor: koll(A,B,C) und A,B,C 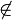 g,
g, 
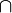 g
g 
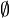 und
und 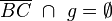
Beh: 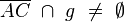
Bew:
1. koll(A,B,C) und A,B,C 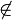 g laut Vor:
g laut Vor:
2. |AB| + |BC| = |AC| laut Ax II/3 Dreiecks ungl.
- Dieser Schritt stimmt so nicht, da eine der drei Gleichungen gelten kann und nicht genau diese. Hier muss man die Fälle unterscheiden.--Tutor Andreas 17:04, 21. Jun. 2012 (CEST)
3. 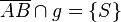 laut Vor.
laut Vor.
4. Zw(A,S,B) laut 3. und trivial
5. |AS| + |SB| = |AB| laut Ax II/3 und 4
6. |AS| + |SB| + |BC| = |AC| laut Rechnen in R, 5. und 2.
7. |AS| + |SC| = |AC| laut Rechnen in R und 6.
8. Zw(A,S,C) laut 7 und Ax II/3
9. Unmittelbar folgt 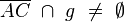 weil
weil 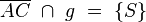 laut 8. und trivial q.e.d --Nemo81 18:55, 14. Jun. 2012 (CEST)
laut 8. und trivial q.e.d --Nemo81 18:55, 14. Jun. 2012 (CEST)