Basiswinkelsatz und Mittelsenkrechtenkriterium (SoSe 12): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 15: | Zeile 15: | ||
===== Satz VII.5: Basiswinkelsatz ===== | ===== Satz VII.5: Basiswinkelsatz ===== | ||
::In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander. | ::In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander. | ||
| − | + | [[Schulvariante des Beweises des Basiswinkelsatzes]] | |
| − | + | ||
| − | + | ||
| − | [[ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
===== Ein im Rahmen unserer Theorie korrekter Beweis des Basiswinkelsatzes ===== | ===== Ein im Rahmen unserer Theorie korrekter Beweis des Basiswinkelsatzes ===== | ||
Version vom 21. Juni 2012, 16:57 Uhr
|
Der BasiswinkelsatzGleichschenklige DreieckeDefinition VII.4 : (gleichschenkliges Dreieck)Das können sie selbst. Bringen Sie in der Definition die Begriffe Basis, Basiswinkel und Schenkel eines gleichschenkligen Dreiecks unter. Übungsaufgabe Der BasiswinkelsatzSatz VII.5: Basiswinkelsatz
Schulvariante des Beweises des Basiswinkelsatzes Ein im Rahmen unserer Theorie korrekter Beweis des BasiswinkelsatzesProbieren Sie ruhig weitere Varianten: Mittelsenkrechte ... .
Letztlich hilft nur die Winkelhalbierende. Damit wir uns auf die wesentliche Beweisidee des Basiwinkelsatzes konzentrieren können, schicken wir ein Lemma voraus. Lemma 1
Beweis von Lemma 1später (Wir haben wichtigeres zu tun.) googeln Sie: "Geschichten aus dem Inneren Gieding" und Sie werden fündig. Beweis des Basiswinkelsatzes
Das MittelsenkrechtenkriteriumSatz VII.6: (Mittelsenkrechtenkriterium)
Bezug zur Schule:Konstruktion der Mittelsenkrechten einer Strecke Konstruktionsvorschrift: gegeben: Strecke gesucht:
Frage: Ist dieser Algorithmus korrekt? Anders gefragt: Ist Wir beweisen die Korrektheit der Konstruktion indem wir folgendes zeigen: Satz VII.6 a: (hinreichende Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von
|
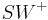 eines Winkels
eines Winkels  schneidet die Strecke
schneidet die Strecke  in genau einem Punkt
in genau einem Punkt  .
.
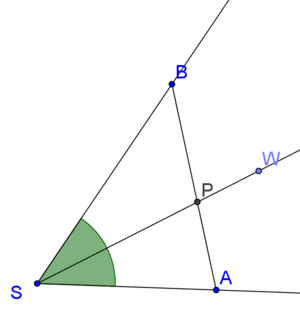
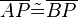 gilt.
gilt.
 , die Mittelsenkrechte von
, die Mittelsenkrechte von  , dessen Radius
, dessen Radius 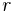 länger als die Hälfte der Länge der Strecke
länger als die Hälfte der Länge der Strecke  .
.
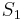 und
und 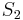 .
.
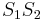 . Sie ist die gesuchte Mittelsenkrechte von
. Sie ist die gesuchte Mittelsenkrechte von 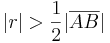 . Wir stellen uns jetzt die frage, ob wir jeden beliebigen Punkt unserer Mittelsenkrechten als Schnittpunkt zweier entsprechender Kreise konstruieren könnten.
. Wir stellen uns jetzt die frage, ob wir jeden beliebigen Punkt unserer Mittelsenkrechten als Schnittpunkt zweier entsprechender Kreise konstruieren könnten.

