|
zurück zu Basiswinkelsatz und Mittelsenkrechtenkriterium SoSe_13
Der folgende Beweis ist für die Schule ok. im Rahmen unserer Theorie jedoch nicht zugelassen
Es sei  ein Dreieck mit den schulüblichen Bezeichnungen. o.B.d.A. seien die Seiten ein Dreieck mit den schulüblichen Bezeichnungen. o.B.d.A. seien die Seiten  und und  kongruent zueinander: kongruent zueinander:
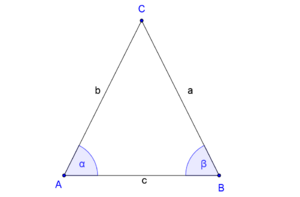
Nach der Existenz und Eindeutigkeit des Mittelpunktes einer Strecke existiert der Mittelpunkt  der Dreiecksseite der Dreiecksseite  . .
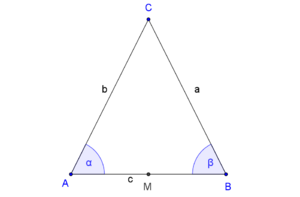
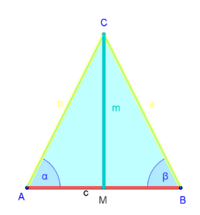
Wir werden jetzt zeigen, dass die beiden Teildreiecke 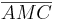 und und 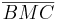 kongruent zueinander sind: kongruent zueinander sind:
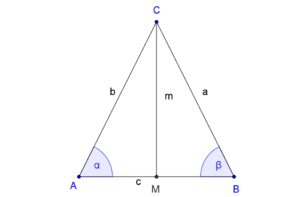
Nachweis von 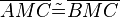 : :
| Nr.
|
Skizze
|
Beweisschritt
|
Begründung
|
| (1)
|
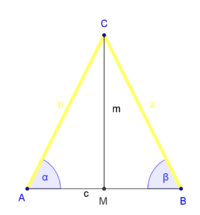
|
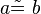
|
Voraussetzung
|
| (2)
|
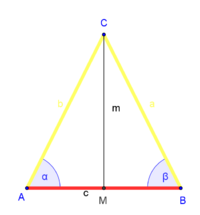
|
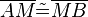
|
 ist Mittelpunkt von ist Mittelpunkt von 
|
| (3)
|
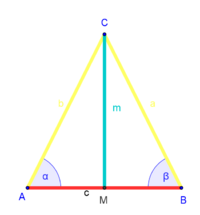
|
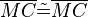
|
trivial (oder Reflexivität der Kongruenzrelation)
|
| (4)
|
|
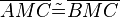
|
(1), (2), (3), SSS
|
Wegen (4) gilt nun auch 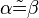 . .
w.z.b.w.
Ein schöner einfacher Beweis, leider hat er hier keine Gültigkeit. Warum?
Der Beweis des Kongruenzsatzes SSS beruht auf dem Basiswinkelsatz.
Daher dürfen wir den Basiswinkelsatz nicht mit dem Kongruenzsatz SSS beweisen.
--Tchu Tcha Tcha 19:21, 21. Jun. 2012 (CEST)
zurück zu Basiswinkelsatz und Mittelsenkrechtenkriterium (SoSe 12)
|  ein Dreieck mit den schulüblichen Bezeichnungen. o.B.d.A. seien die Seiten
ein Dreieck mit den schulüblichen Bezeichnungen. o.B.d.A. seien die Seiten  und
und  kongruent zueinander:
kongruent zueinander:

 der Dreiecksseite
der Dreiecksseite  .
.

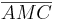 und
und 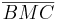 kongruent zueinander sind:
kongruent zueinander sind:

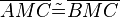 :
:

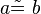

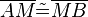

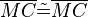

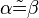 .
.

