Diskussion:Lösung von Aufgabe 8.3P (SoSe 12): Unterschied zwischen den Versionen
| Zeile 5: | Zeile 5: | ||
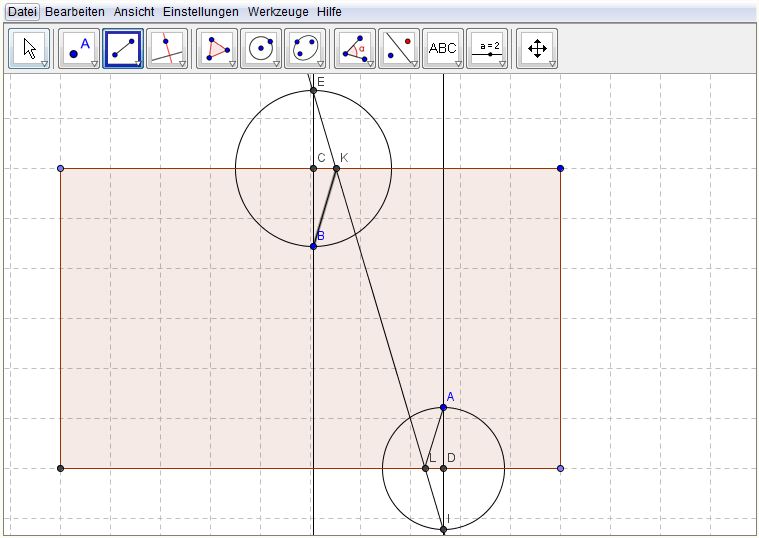
[[Datei:Zwei banden 2.JPG]] | [[Datei:Zwei banden 2.JPG]] | ||
gibt es zwölf mögliche bilder?--[[Benutzer:Studentin|Studentin]] 21:54, 7. Jun. 2012 (CEST) | gibt es zwölf mögliche bilder?--[[Benutzer:Studentin|Studentin]] 21:54, 7. Jun. 2012 (CEST) | ||
| − | <br />Ja, es gibt sogar noch mehr Möglichkeiten. Gut ist, wenn man seine Konstruktionsschritte noch begründen kann.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:50, 19. Jun. 2012 (CEST) | + | <br />Ja, es gibt sogar noch mehr Möglichkeiten. Gut ist, wenn man seine Konstruktionsschritte noch begründen kann.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:50, 19. Jun. 2012 (CEST)<br /><br /> |
| + | insbesondere meine kreise kann ich begründen ;-)) <br /> | ||
| + | ich hab die spiegeln-funktion gar nicht gesehen und bin von lineal und zirkel ausgegangen ;-))<br /> | ||
| + | warum mehr als 12 möglichkeiten?<br /> | ||
| + | wenn ich vier banden a, b, c, d habe, kann ich doch, wenn ich über zwei banden spielen soll über: <br /> | ||
| + | ab, ac, ad<br /> | ||
| + | ba, bc, bd<br /> | ||
| + | und so weiter spielen, also 12 mögliche konstuktionen machen? oder wo liegt mein denkfehler??? | ||
| + | --[[Benutzer:Studentin|Studentin]] 22:23, 21. Jun. 2012 (CEST) | ||
Version vom 21. Juni 2012, 21:23 Uhr
Die nachfolgende GeoGebra-Applikation zeigt einen Billardtisch mit zwei Kugeln in der Draufsicht. Kugel A soll durch einen zentralen Stoß die Kugel B über zwei Banden treffen. Konstruieren und Begründen Sie Ihre Konstruktion.
jetzt nochmal in die andere richtung mit den selben zwei banden:
gibt es zwölf mögliche bilder?--Studentin 21:54, 7. Jun. 2012 (CEST)
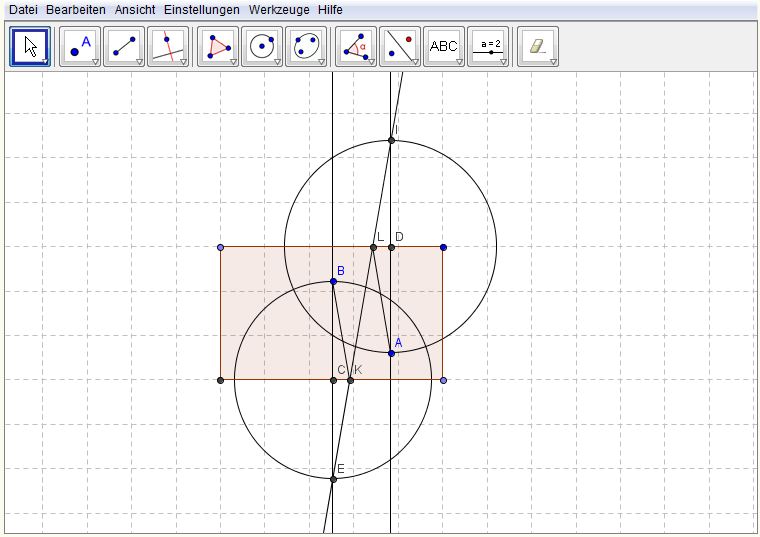
Ja, es gibt sogar noch mehr Möglichkeiten. Gut ist, wenn man seine Konstruktionsschritte noch begründen kann.--Tutorin Anne 11:50, 19. Jun. 2012 (CEST)
insbesondere meine kreise kann ich begründen ;-))
ich hab die spiegeln-funktion gar nicht gesehen und bin von lineal und zirkel ausgegangen ;-))
warum mehr als 12 möglichkeiten?
wenn ich vier banden a, b, c, d habe, kann ich doch, wenn ich über zwei banden spielen soll über:
ab, ac, ad
ba, bc, bd
und so weiter spielen, also 12 mögliche konstuktionen machen? oder wo liegt mein denkfehler???
--Studentin 22:23, 21. Jun. 2012 (CEST)
