Lösung von Aufgabe 6.2: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 23: | Zeile 23: | ||
|} | |} | ||
Mehr Fälle gibt es nach der Vorraussetzung nicht, oder? | Mehr Fälle gibt es nach der Vorraussetzung nicht, oder? | ||
| + | --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] | ||
Version vom 4. Juni 2010, 01:50 Uhr
Das Axiom I.7 sagt aus:
Es gibt vier Punkte, die nicht komplanar sind.
Es sei 
eine beliebige Ebene und 
die vier Punkte entsprechend Axiom I.7. Klassifizieren Sie alle Fälle die bezüglich der Inzidenz der Punkte mit auftreten können.
Vorraussetzung: Die Punkte sind nicht kollinear. Wenn mehr als zwei Punkte kollinear sind (zB. 
Gerade g), dann sind diese Punkte und der verbleibende nichtkollineare Punkt (im Bsp. D) Elemente der Ebene .
Begründung:
Definition I/4: (Inzidenz Gerade Ebene)
Eine Gerade g gehört zu einer Ebene E, wenn jeder Punkt von g zu E gehört.
Axiom I/4
Zu je drei nichtkollinearen Punkten gibt es genau eine Ebene, die diese drei Punkte enthält. (...)
Der Fall, dass alle vier Punkte kollinear sind (also Gerade g) ist dann trivial, da durch Definition I/4 abgedeckt.
| Fall | Bsp/Ausprägung | Zusatz | nKomp |
| DREI Punkte liegen in (sind Elemente von...) |
 |
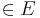mögliche Tripel:  1(A,B,C) 2(A,B,D) 3(A,C,D) 4 (B,C,D) |
1(D) 2(C) 3(B) 4 (A)
|
| VIER Punkte sind komplanar | |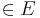
alle Punkte liegen "auf" / "in" Ebene |
keine Punkt nKomp |
Mehr Fälle gibt es nach der Vorraussetzung nicht, oder? --Heinzvaneugen
