Verkettung von drei Geradenspiegelungen SoSe 12: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „=== Verkettung von drei Geradenspiegelungen === Aufgabe: Welche prinzipiellen Möglichkeiten bezüglich der Lage der Achsen gibt es bei der Verkettung von drei Ge…“) |
(→Satz X.2:) |
||
| Zeile 7: | Zeile 7: | ||
=====Satz X.2: ===== | =====Satz X.2: ===== | ||
| − | :Die Verkettung von drei Geradenspiegelungen <math>S_{a}\cir S_{b} \cir S_{c}</math>, an drei Geraden ''a'', ''b'' und ''c'' die sich in einem Punkt ''S'' schneiden (kopunktal), ist eine Geradenspiegelung an einer Achse ''d'', die durch den Punkt ''S'' verläuft mit <math>\angle ab = \angle dc </math>.<br /> | + | :Die Verkettung von drei Geradenspiegelungen <math>S_{a}\cir S_{b} \cir S_{c}</math>, an drei Geraden ''a'', ''b'' und ''c'' die sich in einem Punkt ''S'' schneiden (kopunktal), ist eine Geradenspiegelung an einer Achse ''d'', die durch den Punkt ''S'' verläuft mit <math>\left|\angle ab\right| = \left|\angle dc\right| </math>.<br /> |
Beweis:<br /><br /> | Beweis:<br /><br /> | ||
Version vom 30. Juni 2012, 18:50 Uhr
Verkettung von drei Geradenspiegelungen
Aufgabe: Welche prinzipiellen Möglichkeiten bezüglich der Lage der Achsen gibt es bei der Verkettung von drei Geradenspiegelungen? (gerne auch als Bild).
Satz X.1:
- Die Verkettung von drei Geradenspiegelungen Fehler beim Parsen(Unbekannte Funktion „\cir“): S_{a}\cir S_{b} \cir S_{c}
an zueinander parallelen Geraden a, b und c ist eine Geradenspiegelung an einer Geraden d mitund
.
Beweis:
Satz X.2:
- Die Verkettung von drei Geradenspiegelungen Fehler beim Parsen(Unbekannte Funktion „\cir“): S_{a}\cir S_{b} \cir S_{c}
, an drei Geraden a, b und c die sich in einem Punkt S schneiden (kopunktal), ist eine Geradenspiegelung an einer Achse d, die durch den Punkt S verläuft mit 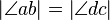 .
.
Beweis:

