Lösung von Aufgabe 9.2 S: Unterschied zwischen den Versionen
(→Kopernikus / Just noch ein sailA) |
(→(b) Vorschlag 1) |
||
| Zeile 54: | Zeile 54: | ||
|- | |- | ||
| 2 | | 2 | ||
| − | | <math>\exists \angle CBD | + | | <math>\exists \angle CBD \ :\left| \angle ABC \right| =\left| \angle CBD \right|</math> |
| 1, Def. rechter Winkel | | 1, Def. rechter Winkel | ||
|- | |- | ||
| 3 | | 3 | ||
| <math>\left| \angle ABC \right| +\left| \angle CBD \right| =180</math> | | <math>\left| \angle ABC \right| +\left| \angle CBD \right| =180</math> | ||
| − | | 2,Axiom IV/7( | + | | 2,Axiom IV/7(Supplementaxiom), Def. V/7 Supplementärwinkel |
|- | |- | ||
| 4 | | 4 | ||
| Zeile 76: | Zeile 76: | ||
--[[Benutzer:Kopernikus|Kopernikus]] 17:00, 25. Jun. 2012 (CEST)<br /> | --[[Benutzer:Kopernikus|Kopernikus]] 17:00, 25. Jun. 2012 (CEST)<br /> | ||
--[[Benutzer:Just noch ein sailA|Just noch ein sailA]] 17:00, 25. Jun. 2012 (CEST)<br /> | --[[Benutzer:Just noch ein sailA|Just noch ein sailA]] 17:00, 25. Jun. 2012 (CEST)<br /> | ||
| + | * Der Beweis scheint mir bis auf weniges logisch. Warum wird <math>\left| \angle ABC \right| = 90 =\left| \angle CBA \right|</math> geschrieben? <math>\angle CBA</math> ist doch genau der selbe Winkel wie <math>\angle ABC</math>... --[[Benutzer:Andreas|Tutor Andreas]] 18:03, 1. Jul. 2012 (CEST) | ||
Version vom 1. Juli 2012, 17:03 Uhr
Satz:
Jeder rechte Winkel hat das Maß 90.
a) Formulieren Sie mit "wenn...dann..."
b) Beweisen Sie den Satz.
a) "Wenn ein Winkel ein rechter Winkel ist, dann hat er das Maß 90."--Tchu Tcha Tcha 16:34, 20. Jun. 2012 (CEST)
b)
direkter Beweis:
Nach der Definition Rechter Winkel gilt: Wenn ein Winkel dieselbe Größe wie einer seiner Nebenwinkel hat, so ist er ein rechter Winkel.
also: Rechter Winkel, nur wenn gilt: 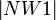 =
= 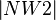 (1) // (NW1 steht hier für NebenWinkel1...)
(1) // (NW1 steht hier für NebenWinkel1...)
Nach dem Supplementaxiom (IV.4) wissen wir: Nebenwinkel sind supplementär.
also können wir durch die Def. supplementär folgern, dass 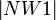 +
+ 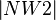 =180 (2) gelten muss.
=180 (2) gelten muss.
Da nach (1) gilt 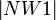 =
= 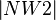 können wir (2) auch so schreiben:
können wir (2) auch so schreiben:
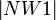 +
+ 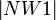 =180
=180
nach Rechnen in R folgt: 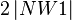 =180
=180
nach Rechnen in R folgt weiter: 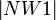 =90
=90
 nach (1) gilt außerdem:
nach (1) gilt außerdem: 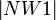 =
= 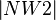
Jeder rechte Winkel muss das Maß 90 haben.
qed.
--Tchu Tcha Tcha 18:21, 20. Jun. 2012 (CEST)
korrekter Beweis --*m.g.* 13:39, 23. Jun. 2012 (CEST)
Wenn Sie die Idizes tief stellen wollen; Der Unterstrich hilft: NW_1
Kopernikus / Just noch ein sailA
(a) Vorschlag 1
Wenn ein Winkel ein rechter ist, dann hat er das Maß 90.
(b) Vorschlag 1
Vor:  ist rechter Winkel
ist rechter Winkel
Beh.: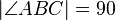
Direkter Beweis
| Schritt | Beweis | Begründung |
|---|---|---|
| 1 |  ist rechter Winkel ist rechter Winkel
|
Vor. |
| 2 | 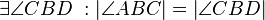
|
1, Def. rechter Winkel |
| 3 | 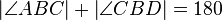
|
2,Axiom IV/7(Supplementaxiom), Def. V/7 Supplementärwinkel |
| 4 | 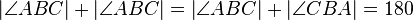
|
2,3 |
| 5 | 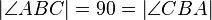
|
Rechnen in R |
| 6 | q.e.d | 5, Vor. |
--Kopernikus 17:00, 25. Jun. 2012 (CEST)
--Just noch ein sailA 17:00, 25. Jun. 2012 (CEST)
- Der Beweis scheint mir bis auf weniges logisch. Warum wird
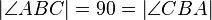 geschrieben?
geschrieben? 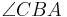 ist doch genau der selbe Winkel wie
ist doch genau der selbe Winkel wie  ... --Tutor Andreas 18:03, 1. Jul. 2012 (CEST)
... --Tutor Andreas 18:03, 1. Jul. 2012 (CEST)

