Lösung von Aufgabe 10.6 S: Unterschied zwischen den Versionen
| Zeile 17: | Zeile 17: | ||
(8) <math>\left|\overline{AM} \right| = \left|\overline{MC} \right| \wedge \left|\overline{BM} \right| = \left|\overline{MD} \right|</math>// (7), Dreieckskongruenz<br /> | (8) <math>\left|\overline{AM} \right| = \left|\overline{MC} \right| \wedge \left|\overline{BM} \right| = \left|\overline{MD} \right|</math>// (7), Dreieckskongruenz<br /> | ||
qed<br /> | qed<br /> | ||
| − | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 18:55, 28. Jun. 2012 (CEST) | + | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 18:55, 28. Jun. 2012 (CEST)<br /> |
| + | Ich habe noch ein paar Kleinigkeiten verändert, aber ansonsten völlig nachvollziehbar und korrekt. | ||
| + | Kleinigkeiten: | ||
| + | <math>\left|\overline{AC} \right| = \left|\overline{AC} \right|</math> hier entweder <math>\overline {AC} \tilde {=} \overline {AC} </math> ODER |AC| = |AC|--[[Benutzer:Andreas|Tutor Andreas]] 19:47, 1. Jul. 2012 (CEST) | ||
Version vom 1. Juli 2012, 18:47 Uhr
Lösungsversuch Nummero6/Tchu Tcha Tcha:
a)Parallelogramme.
Def. (Parallelogramm): Ein Viereck, bei dem die gegenüberliegenden Seiten jeweils gleichlang sind, nennt man Parallelogramm.
b)Wenn ein Viereck ein Parallelogramm ist, dann halbieren sich seine Diagonalen.
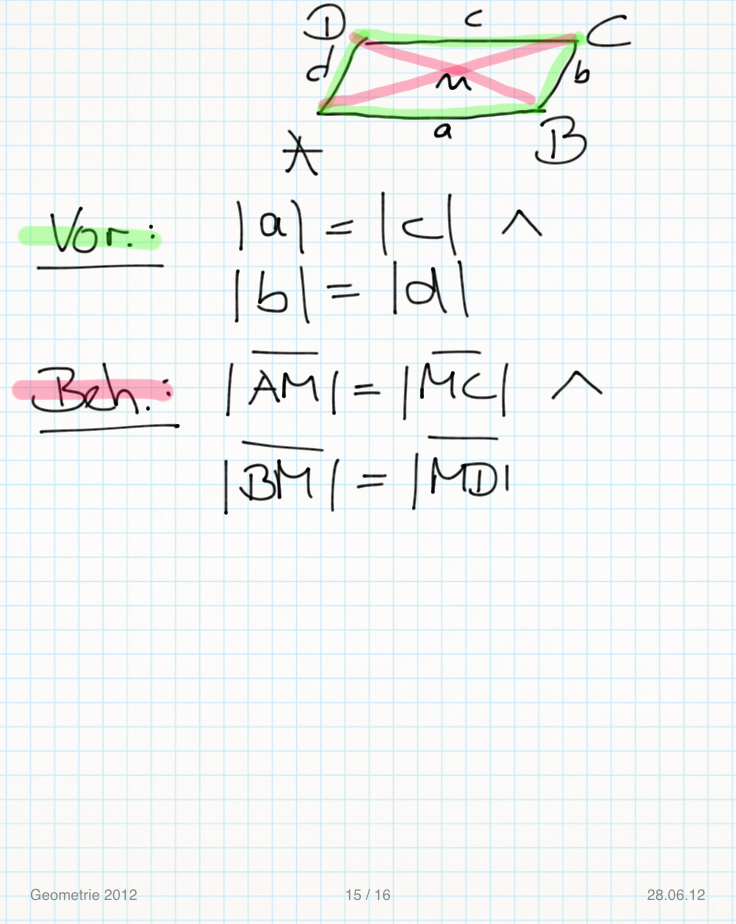
(1) 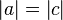 // Voraussetzung
// Voraussetzung
(2) 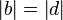 // Voraussetzung
// Voraussetzung
(3) 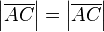 // trivial
// trivial
(4) 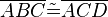 // (1-3), SSS
// (1-3), SSS
(4a) 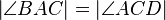 // (4), Dreieckskongruenz
// (4), Dreieckskongruenz
(5) 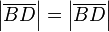 // trivial
// trivial
(6) 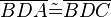 // (1), (2), (5), SSS
// (1), (2), (5), SSS
(6a) 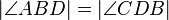 // (6), Dreieckskongruenz
// (6), Dreieckskongruenz
(7) 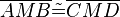 // (1), (4a), (6a), WSW
// (1), (4a), (6a), WSW
(8) 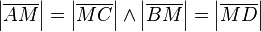 // (7), Dreieckskongruenz
// (7), Dreieckskongruenz
qed
--Tchu Tcha Tcha 18:55, 28. Jun. 2012 (CEST)
Ich habe noch ein paar Kleinigkeiten verändert, aber ansonsten völlig nachvollziehbar und korrekt.
Kleinigkeiten:
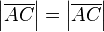 hier entweder
hier entweder 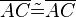 ODER |AC| = |AC|--Tutor Andreas 19:47, 1. Jul. 2012 (CEST)
ODER |AC| = |AC|--Tutor Andreas 19:47, 1. Jul. 2012 (CEST)

