Lösung von Aufgabe 6.10: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
|||
| Zeile 1: | Zeile 1: | ||
Der folgende Satz bezieht sich auf die ebene Geometrie.<br /> | Der folgende Satz bezieht sich auf die ebene Geometrie.<br /> | ||
<u>'''Satz:'''</u><br /> | <u>'''Satz:'''</u><br /> | ||
| − | ::Es seien <math>\ k_1</math> und <math>\ k_2</math> zwei Kreise mit den Mittelpunkten <math>\ M_1</math> bzw. <math>\ M_2</math> und den Radien <math>\ r_1</math> bzw. <math>\ r_2</math>. <br />Die Kreise <math>\ k_1</math> und <math>\ k_2</math> haben dann und nur dann einen und nur einen Punkt <math>\ S</math> gemeinsam, wenn <math>\ |M_1M_2|=|r_1|+|r_2|</math> gilt. | + | ::Es seien <math>\ k_1</math> und <math>\ k_2</math> zwei Kreise mit den Mittelpunkten <math>\ M_1</math> bzw. <math>\ M_2</math> und den Radien <math>\ r_1</math> bzw. <math>\ r_2</math>. |
| + | <br />Die Kreise <math>\ k_1</math> und <math>\ k_2</math> haben dann und nur dann einen und nur einen Punkt <math>\ S</math> gemeinsam, wenn <math>\ |M_1M_2|=|r_1|+|r_2|</math> gilt. | ||
# Formulieren Sie den Satz ohne die Verwendung der Phrasen <span style="color: green">''dann und nur dann''</span> sowie <span style="color: green">''einen und nur einen''</span>. | # Formulieren Sie den Satz ohne die Verwendung der Phrasen <span style="color: green">''dann und nur dann''</span> sowie <span style="color: green">''einen und nur einen''</span>. | ||
# Sie haben sicherlich erkannt, dass es sich bei dem Satz um eine Äquivalenz handelt. Formulieren Sie die beiden Implikationen, die diese Äquivalenz beinhaltet. | # Sie haben sicherlich erkannt, dass es sich bei dem Satz um eine Äquivalenz handelt. Formulieren Sie die beiden Implikationen, die diese Äquivalenz beinhaltet. | ||
| − | # | + | # Beweisen Sie die beiden Implikationen. |
| + | |||
| + | |||
| + | |||
| + | # Reicht es, wenn man mit "genau" arbeitet? | ||
| + | <br />Die Kreise <math>\ k_1</math> und <math>\ k_2</math> haben '''genau''' dann '''genau''' einen Punkt <math>\ S</math> gemeinsam, wenn <math>\ |M_1M_2|=|r_1|+|r_2|</math> gilt. | ||
| + | # I) Wenn <math>\ |M_1M_2|=|r_1|+|r_2|</math> gilt, dann haben die beiden Kreise <math>\ k_1</math> und <math>\ k_2</math> genau einen Punkt gemeinsam, den Berührpunkt S. | ||
| + | <br />II) Wenn zwei Kreise <math>\ k_1</math> und <math>\ k_2</math> genau einen Punkt gemeinsam haben, so gilt <math>\ |M_1M_2|=|r_1|+|r_2|</math> | ||
| + | # Beweisen Sie die beiden Implikationen. | ||
| + | <br />I) | ||
| + | Vo | ||
| + | <br />II) | ||
Version vom 4. Juni 2010, 03:30 Uhr
Der folgende Satz bezieht sich auf die ebene Geometrie.
Satz:
- Es seien
und 
zwei Kreise mit den Mittelpunkten 
bzw.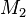 
und den Radien 
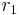bzw.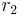 
.
- Es seien
Die Kreise und haben dann und nur dann einen und nur einen Punkt 
gemeinsam, wenn 
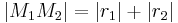gilt.
- Formulieren Sie den Satz ohne die Verwendung der Phrasen dann und nur dann sowie einen und nur einen.
- Sie haben sicherlich erkannt, dass es sich bei dem Satz um eine Äquivalenz handelt. Formulieren Sie die beiden Implikationen, die diese Äquivalenz beinhaltet.
- Beweisen Sie die beiden Implikationen.
- Reicht es, wenn man mit "genau" arbeitet?
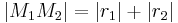Die Kreise und haben genau dann genau einen Punkt gemeinsam, wenn gilt.
- I) Wenn 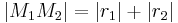gilt, dann haben die beiden Kreise und genau einen Punkt gemeinsam, den Berührpunkt S.
II) Wenn zwei Kreise und genau einen Punkt gemeinsam haben, so gilt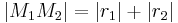
- Beweisen Sie die beiden Implikationen.
I)
Vo
II)
