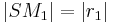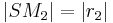Lösung von Aufgabe 6.10
Der folgende Satz bezieht sich auf die ebene Geometrie.
Satz:
- Es seien
 und
und  zwei Kreise mit den Mittelpunkten
zwei Kreise mit den Mittelpunkten  bzw.
bzw. 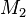 und den Radien
und den Radien 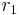 bzw.
bzw. 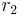 . Keiner der Mittelpunkte möge dabei im Inneren des jeweils anderen Kreises liegen.
. Keiner der Mittelpunkte möge dabei im Inneren des jeweils anderen Kreises liegen.
- Es seien
- Die Kreise
 und
und  haben dann und nur dann einen und nur einen Punkt
haben dann und nur dann einen und nur einen Punkt  gemeinsam, wenn
gemeinsam, wenn 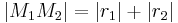 gilt.
gilt.
- Die Kreise
- Formulieren Sie den Satz ohne die Verwendung der Phrasen dann und nur dann sowie einen und nur einen.
- Sie haben sicherlich erkannt, dass es sich bei dem Satz um eine Äquivalenz handelt. Formulieren Sie die beiden Implikationen, die diese Äquivalenz beinhaltet.
- Beweisen Sie die beiden Implikationen.
Inhaltsverzeichnis |
Lösung der Aufgabe --*m.g.* 09:08, 21. Jun. 2010 (UTC)
Teilaufgabe 1
Die Formulierung "eine und nur eine" ist äquivalent zu "genau eine".
Die Lösung von Heinzvaneugen kann also 1 zu 1 übernommen werden:
Die Kreise  und
und  haben genau dann genau einen Punkt
haben genau dann genau einen Punkt  gemeinsam, wenn
gemeinsam, wenn 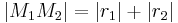 gilt.
gilt.
Teilaufgabe 2
Die Lösung von Heinzvaneugen ist korrekt.
allgemeiner Teil für beide Implikationen
Es seien  und
und  zwei Kreise mit den Mittelpunkten
zwei Kreise mit den Mittelpunkten  bzw.
bzw. 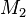 und den Radien
und den Radien 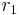 bzw.
bzw. 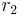 .
.
Implikation I (-->)
Wenn 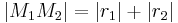 , dann haben die beiden Kreise
, dann haben die beiden Kreise  und
und  genau einen Punkt gemeinsam.
genau einen Punkt gemeinsam.
andere möglich Formulierung (neben vielen weiteren, die hier nicht alle aufgezeigt werden sollen und können):
Wenn für zwei Kreise gilt, dass die Summe der Längen ihrer Radien gleich dem Abstand ihrer Mittelpunkte ist, dann existiert genau ein Punkt  , den die beiden Kreise gemeinsam haben.
, den die beiden Kreise gemeinsam haben.
(Der allgemein Teil zuvor ist hier mit aufgenommen und hätte nicht extra formuliert werden müssen.)
Implikation II (<--)
Wenn  und
und  genau einen Punkt gemeinsam haben, so gilt
genau einen Punkt gemeinsam haben, so gilt 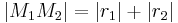 .
.
Bemerkung zu der Formulierung von Heinzvaneugen:
Sie formulieren: Wenn zwei Kreise  und
und  ... .
... .
Die beiden Kreise wurden aber vorab schon festgelegt. Es seien  und
und  ... . Jetzt bleiben wir natürlich in den weiteren Formulierungen bei diesen zunächst beliebigen, dann aber festen Kreisen. Also besser: Wenn die Kreise
... . Jetzt bleiben wir natürlich in den weiteren Formulierungen bei diesen zunächst beliebigen, dann aber festen Kreisen. Also besser: Wenn die Kreise  und
und  ... . Oder: Wenn
... . Oder: Wenn  und
und  ... .
... .
Teilaufgabe 3
Beweis von Implikation I
Voraussetzung
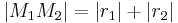
Behauptung 1 (Existenzaussage)
Es gibt einen Punkt  , der sowohl zu
, der sowohl zu  als auch zu
als auch zu  gehört.
gehört.
Behauptung 2 (Eindeutigkeitsaussage)
Es gibt nicht mehr als einen Punkt  den
den  und
und  gemeinsam haben.
gemeinsam haben.
Beweis der Existenzaussage (Behauptung 1)
Nachzuweisen ist die Existenz eines Punktes  der sowohl zu
der sowohl zu  als auch zu
als auch zu  gehört.
gehört.
Der Kreis  ist die Menge aller Punkte unserer Ebene, die zu dem Punkt
ist die Menge aller Punkte unserer Ebene, die zu dem Punkt  den Abstand
den Abstand 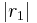 haben.
haben.
Der Kreis  ist die Menge aller Punkte unserer Ebene, die zu dem Punkt
ist die Menge aller Punkte unserer Ebene, die zu dem Punkt 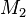 den Abstand
den Abstand 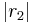 haben.
haben.
Wir haben also die Existenz eines Punktes nachzuweisen, für den gilt:
nachzuweisen, für den gilt:
und
Wir konstruieren uns einen solchen Punkt  wie folgt:
wie folgt:
Wir gehen von dem Strahl 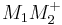 aus.
aus.
Auf 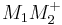 gibt es nach dem Axiom vom Lineal genau einen Punkt
gibt es nach dem Axiom vom Lineal genau einen Punkt  , der zu
, der zu  den Abstand
den Abstand 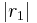 hat:
hat: 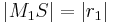
Jetzt gilt: (*) Der Punkt  liegt zwischen den Punkten
liegt zwischen den Punkten  und
und 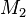
Begründung von (*):
- Der Punkt
 fällt nicht mit
fällt nicht mit  zusammen:
zusammen: 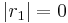 , entarteter Kreis.
, entarteter Kreis.
- Der Punkt
 fällt nicht mit
fällt nicht mit 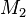 zusammen: entsprechend der Voraussetzung würde jetzt
zusammen: entsprechend der Voraussetzung würde jetzt  entarten.
entarten.
- Annahme:
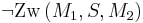
- Unter Berücksichtigung der Tatsache, dass
 ein Punkt der Halbgeraden
ein Punkt der Halbgeraden 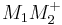 ist, kann jetzt nur noch
ist, kann jetzt nur noch 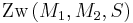 gelten:
gelten:
- Der Punkt
-
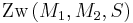 bedeutet: (**)
bedeutet: (**) 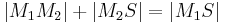
- Der Punkt
 wurde so gewählt, dass sein Abstand
wurde so gewählt, dass sein Abstand 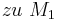 die Zahl
die Zahl 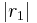 ist, womit (**) auch wie folgt geschrieben werden kann:
ist, womit (**) auch wie folgt geschrieben werden kann:
- (***)
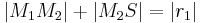
- Unter Berücksichtigung der Voraussetzung
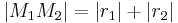 gilt entsprechend (***) auch (****)
gilt entsprechend (***) auch (****) 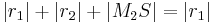
- Da nun
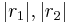 und
und 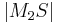 positive reelle Zahlen sind, ist (****) ein Widerspruch in sich. Die Annahme
positive reelle Zahlen sind, ist (****) ein Widerspruch in sich. Die Annahme 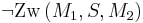
ist zu verwerfen.
-
Nach diesen Ausführungen können wir also davon ausgehen, dass der von uns konstruierte Punkt  zwischen den Punkten
zwischen den Punkten  und
und 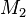 liegt. Aus
liegt. Aus 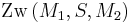 folgt:
folgt:
(i) 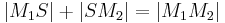
Unter Berücksichtigung der Voraussetzung 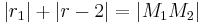 läßt sich (i) als
läßt sich (i) als
(ii) 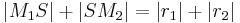
schreiben.
Da  so gewählt wurde, dass
so gewählt wurde, dass 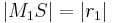 gilt, ist auch
gilt, ist auch
(iii) 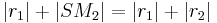
gültig.
Aus (iii) folgt unmittelbar 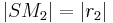 .
.
Damit gehört der Punkt  sowohl zu
sowohl zu  als auch zu
als auch zu  .
.
Die Existenz des gemeinsamen Punktes  der beiden Kreise
der beiden Kreise  und
und  ist damit nachgewiesen.
ist damit nachgewiesen.
Beweis der Eindeutigkeitsaussage (Behauptung 2)
Annahme: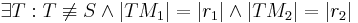
Wegen 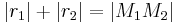 und
und 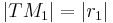 und
und 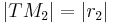 gilt:
gilt:
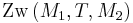
und damit natürlich auch
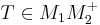
Damit sind  und
und  zwei verschiedene Punkte auf dem Strahl
zwei verschiedene Punkte auf dem Strahl 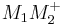 die zum Anfangspunkt dieses Strahls ein und denselben Abstand
die zum Anfangspunkt dieses Strahls ein und denselben Abstand 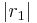 haben.
haben.
Das wäre allerdings ein Widerspruch zur Eindeutigkeitsaussage des Axioms vom Lineal.
Zum Beweis von Heinzvaneugen
Sie wollen beweisen: Aus 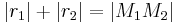 folgt, dass die beiden Kreise genau einen Punkt gemeinsam haben.
Sie führen den Beweis indirekt und negieren bei Beibehaltung der Voraussetzung die Behauptung. Das ist korrekt, so führt man vom Prinzip her indirekte Beweise. Unsere Behauptung besteht eigentlich aus zwei Aussagen: Die beiden Kreise haben einen Punkt gemeinsam und zwar nur einen. Sie negieren die Behauptung korrekt. Die Negation von Die beiden Kreise haben genau einen Punkt gemeinsam ist Die beiden Kreise haben nicht genau einen Punkt gemeinsam. Letzteres bedeutet, dass die beiden Kreise entweder überhaupt keinen Punkt gemeinsam haben (Negation der Existenzaussage) oder dass sie mehr als einen Punkt gemeinsam haben (Negation der Eindeutigkeitsaussage). Das sind in der Tat Ihre beiden Gegenannahmen. Bis hier hin ist alles in Ordnung.
folgt, dass die beiden Kreise genau einen Punkt gemeinsam haben.
Sie führen den Beweis indirekt und negieren bei Beibehaltung der Voraussetzung die Behauptung. Das ist korrekt, so führt man vom Prinzip her indirekte Beweise. Unsere Behauptung besteht eigentlich aus zwei Aussagen: Die beiden Kreise haben einen Punkt gemeinsam und zwar nur einen. Sie negieren die Behauptung korrekt. Die Negation von Die beiden Kreise haben genau einen Punkt gemeinsam ist Die beiden Kreise haben nicht genau einen Punkt gemeinsam. Letzteres bedeutet, dass die beiden Kreise entweder überhaupt keinen Punkt gemeinsam haben (Negation der Existenzaussage) oder dass sie mehr als einen Punkt gemeinsam haben (Negation der Eindeutigkeitsaussage). Das sind in der Tat Ihre beiden Gegenannahmen. Bis hier hin ist alles in Ordnung.
Jetzt kommt der eigentliche Beweis. Sie wählen auf der Strecke 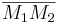 einen ominösen Punkt
einen ominösen Punkt  . Den wird es sicherlich geben (Axiom vom Lineal). Jetzt kommt der Knackpunkt ihres Beweises. Ihre Gegenannahme 1 besagt, dass die beiden Kreise keinen Punkt gemeinsam haben. Damit, so folgern Sie (und soweit ist das auch korrekt), kann der Punkt
. Den wird es sicherlich geben (Axiom vom Lineal). Jetzt kommt der Knackpunkt ihres Beweises. Ihre Gegenannahme 1 besagt, dass die beiden Kreise keinen Punkt gemeinsam haben. Damit, so folgern Sie (und soweit ist das auch korrekt), kann der Punkt  definitiv nicht gleichzeitig zu den beiden Kreisen
definitiv nicht gleichzeitig zu den beiden Kreisen  und
und  gehören. Was heißt aber
gehören. Was heißt aber  gehört nicht gleichzeitig zu
gehört nicht gleichzeitig zu  und zu
und zu  ?
?
-
 gehört zu
gehört zu  aber nicht zu
aber nicht zu 
-
 gehört zu
gehört zu  aber nicht zu
aber nicht zu 
-
 gehört weder zu
gehört weder zu  noch zu
noch zu 
Fall 3 lässt wieder in Unterfälle aufdröseln:
-
 liegt sowohl außerhalb von
liegt sowohl außerhalb von  als auch von
als auch von  . (
. (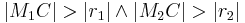 )
)
-
 liegt innerhalb von
liegt innerhalb von  und außerhalb von
und außerhalb von  .(
.(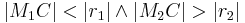 )
)
-
 liegt außerhalb von
liegt außerhalb von  und innerhalb von
und innerhalb von  .(
.(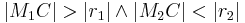 )
)
-
 liegt sowohl innerhalb von
liegt sowohl innerhalb von  als auch innerhalb von
als auch innerhalb von  .(
.(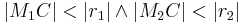 )
)
Sie berücksichtigen in Ihrem Beweis hinsichtlich der Gegenbehauptung 1 nur den Fall 3.1. Das reicht nicht, um diese Gegenbehauptung ad absurdum zu führen.
Genug der Negativdiskussion:
- Sie haben den Teil des Beweises, der sich auf Fall 3.1 bezieht absolut korrekt geführt. Alle weiteren Fälle würde man sicherlich in gewisser Weise analog führen.
Schreiben Sie also in Ihren Teilbeweis (Negation der Existenz): andere Fälle: analog (der Leser überzeuge sich davon).
- Sie haben eine sehr wichtige Erfahrung gemacht. Diese Erfahrung ist letztlich viel wichtiger als der gesamte korrekte Beweis. Weil Sie versuchten einen Existenzbeweis indirekt zu führen, haben Sie sich das Leben etwas zu schwer gemacht. Ich will und kann hier keine Regel aufstellen: Existenzbeweise führt man besser immer direkt. Es mag auch Fälle geben, in denen ein indirekter Existenzbeweis eleganter als die direkte Methode ist. Aber in der größten Zahl der Fälle führt der direkte Existenzbeweis schneller zum Ziel.
Was ist ein Existenzbeweis? Man hat nachzuweisen, dass es bestimmte Repräsentanten eines Begriffs gibt. Dieser Nachweis ist letzlich eine Konstruktionsaufgabe. Insbesondere dann, wenn man vorab schon überzeugt davon ist, dass entsprechende Repräsentanten wirklich existieren, wird man wohl eher damit beginnen, einen solchen Repräsentanten zu konstruieren, als zu versuchen nachzuweisen, dass die Aussage "Meine Konstruktionsaufgabe ist nicht lösbar" falsch ist.
Die Idee, bei Existenzbeweisen erst mal einen direkten Beweis zu versuchen, ist eine heuristische Regel. Heuristik ist vor allem Erfahrung. Erfahrungen muss man vor allem selbst machen. Natürlich kann man von den Erfahrungen anderer profitieren, aber die eigene Erfahrung ist sicherlich nachhaltiger.
Beweis der Implikation II
muss noch geschrieben werden, allein mir fehlt momentan die Zeit, in der nächsten freien Minute (eher Stunde) werde ich das Schreiben der Lösung fortsetzen.--*m.g.* 13:17, 21. Jun. 2010 (UTC)
bisherige Diskussionen
1. Reicht es, wenn man mit "genau" arbeitet?
Die Kreise  und
und  haben genau dann genau einen Punkt
haben genau dann genau einen Punkt  gemeinsam, wenn
gemeinsam, wenn 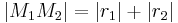 gilt.
gilt.
2. I) Wenn 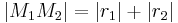 gilt, dann haben die beiden Kreise
gilt, dann haben die beiden Kreise  und
und  genau einen Punkt gemeinsam, den Berührpunkt S.
genau einen Punkt gemeinsam, den Berührpunkt S.
II) Wenn zwei Kreise  und
und  genau einen Punkt gemeinsam haben, so gilt
genau einen Punkt gemeinsam haben, so gilt 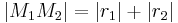
3. Beweisen Sie die beiden Implikationen Teil 1
I)
- Skizze
- Vorraussetzung: Die Strecke
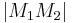 ist so lang wie die Summe der beiden Radien
ist so lang wie die Summe der beiden Radien 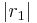 und
und 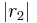 .
.
- Behauptung: Die beiden Kreisen haben genau einen gemeinsamen Punkt.
- Gegen-Behauptung (1): Es gibt KEINEN gemeinsamen Punkt
- Gegen-Behauptung (2): Es gibt MEHR ALS EINEN gemeinsamen Punkt.
- Indirekter Beweis:
- (1) Die Strecke
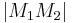 setzt sich zusammen aus den Strecken
setzt sich zusammen aus den Strecken 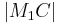 und
und 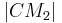 , wobei
, wobei  zwischen
zwischen  und
und 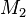 liegt. (Definition II.1: (Zwischenrelation): Ein Punkt
liegt. (Definition II.1: (Zwischenrelation): Ein Punkt  liegt zwischen zwei Punkten
liegt zwischen zwei Punkten  und
und  , wenn
, wenn  gilt (...) ).
gilt (...) ).
- Dieser Punkt C liegt "außerhalb" beider Kreise (Gegen-Behauptung (1) )
- Dadurch ist die Strecke
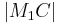 größer als der Radius von
größer als der Radius von  , und die Strecke
, und die Strecke 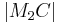 größer als der Radius von
größer als der Radius von  (
(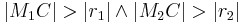 )
)
- Daraus resultiert:
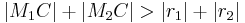 (Widerspruch zu Vorraussetzung und Schritt 1, da
(Widerspruch zu Vorraussetzung und Schritt 1, da 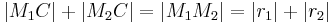 )
)
- (2) Analog, nur bei der Strecken-Ungleichung muss dann der Radius jeweils größer als die Strecke
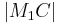 bzw.
bzw.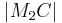 sein. (
sein. (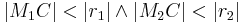 )
)
- (1) Die Strecke
- Dadurch haben wir beweiesen, dass Gegen-Behauptung (1) und (2) zu Widersprüchen führen und nur die Behauptung "Die beiden Kreisen haben genau einen gemeinsamen Punkt" gültig ist. Oder...?
3. Beweisen Sie die beiden Implikationen Teil 2
II)....
--Heinzvaneugen