Lösung von Aufg. 10.3 S: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Kopernikus / Just noch ein sailA)
 
Zeile 45: Zeile 45:
 
--[[Benutzer:Kopernikus|Kopernikus]] 15:21, 28. Jun. 2012 (CEST)<br />
 
--[[Benutzer:Kopernikus|Kopernikus]] 15:21, 28. Jun. 2012 (CEST)<br />
 
--[[Benutzer:Just noch ein sailA|Just noch ein sailA]] 15:21, 28. Jun. 2012  (CEST)<br /><br />
 
--[[Benutzer:Just noch ein sailA|Just noch ein sailA]] 15:21, 28. Jun. 2012  (CEST)<br /><br />
 +
*Passt! --[[Benutzer:Andreas|Tutor Andreas]] 10:58, 10. Jul. 2012 (CEST)
  
 
<br />
 
<br />

Aktuelle Version vom 10. Juli 2012, 09:58 Uhr

Kopernikus / Just noch ein sailA

Beweisen Sie Satz VII.6 b

Wenn ein Punkt \ P zur Mittelsenkrechten der Strecke \overline{AB} gehört, dann hat er zu den Punkten \ A und \ B ein und denselben Abstand.

Vor:
1. 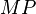\ MP ist Mittelsenkrechte von \overline{AB}

2. \overline{AB}
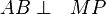
3. \ AB \perp \ \ MP

Beh:
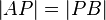
\left| AP \right| =\left| PB \right|

Schritt Beweis Begründung
1 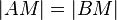\left| AM \right| =\left| BM \right| Vor; Def. Mittelsenkrechte.
2 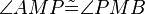\angle AMP \tilde {=} \angle PMB Axiom IV.4, Def. V.7
3 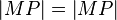\left| MP \right| =\left| MP \right| trivial
4 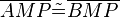\overline {AMP} \tilde {=} \overline {BMP} SWS, (1),(2),(3)
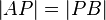
5 \left| AP \right| =\left| PB \right|


--Kopernikus 15:21, 28. Jun. 2012 (CEST)
--Just noch ein sailA 15:21, 28. Jun. 2012 (CEST)


Lösungsversuch Nummero6/Tchu Tcha Tcha

Vor.: 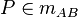P \in m_{AB}
Beh.: 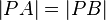\left| PA \right| = \left| PB \right|

(1) 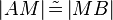\left| AM \right| \tilde {=} \left| MB \right| // Vor., Def. Mittelsenkrechte, Def. Mittelpunkt
(2) 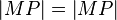\left| MP \right| =\left| MP \right| // trivial
(3) 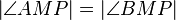\left| \angle AMP \right| = \left| \angle BMP \right| // Vor., Def. Mittelsenkrechte, Def. senkrecht
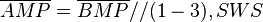
(4) \overline{AMP} = \overline{BMP} // (1-3), SWS
(5) 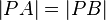\left| PA \right| = \left| PB \right| // (4), Dreieckskongruenz
qed
--Tchu Tcha Tcha 12:24, 30. Jun. 2012 (CEST)
Korrekt!--Tutor Andreas 19:30, 1. Jul. 2012 (CEST)



Lösungsversuch schokomuffin

Vor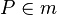P \in m : m = Mittelsenkrechte von \overline{AB}

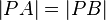
Beh: \left| PA \right| = \left| PB \right|


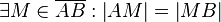(1) \exists M \in \overline{AB}  : \left| AM \right| = \left| MB \right| // Ex.Eind. Mittelpunkt, Ax II.2

(2) 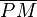\overline{PM} // Vor

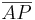(3) \overline{AP} // Ax. vom Lineal

(4) 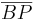\overline{BP} // Ax. vom Lineal

(5) 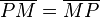\overline{PM} = \overline{MP} // trivial

(6) 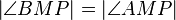\left| \angle BMP \right| = \left| \angle AMP \right| // Def. RW, NW, Vor

(7) 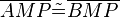\overline{AMP} \tilde {=} \overline{BMP} // SWS (1), (5), (6)

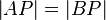(8) \left| AP \right| = \left| BP \right| // Def. Dreieckskongurenz, (7)


--schokomuffin 14:23, 01. Jul. 2012 (CEST)

  • Ich verstehe die Schritte 2,3,4 nicht... warum werden sie gemacht und was sollen sie bedeuten? Außerdem werden sie im Beweis nicht benutzt, was sie überflüssig macht. Ohne diese Schritte finde ich den Beweis gut :) --Tutor Andreas 19:34, 1. Jul. 2012 (CEST)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._10.3_S&oldid=16327“