Lösung von Aufg. 11.4 S: Unterschied zwischen den Versionen
| Zeile 25: | Zeile 25: | ||
(4) Widerspruch zur Voraussetzung, Annahme 2 ist zu verwerfen // (3), Vor.<br /> | (4) Widerspruch zur Voraussetzung, Annahme 2 ist zu verwerfen // (3), Vor.<br /> | ||
(5) Behauptung stimmt. // (2),(4)<br /> | (5) Behauptung stimmt. // (2),(4)<br /> | ||
| − | qed.<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 13:37, 9. Jul. 2012 (CEST) | + | qed.<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 13:37, 9. Jul. 2012 (CEST)<br /> |
| + | *Sieht gut aus und ist kurz und knapp :) --[[Benutzer:Andreas|Tutor Andreas]] 11:20, 10. Jul. 2012 (CEST) | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 10. Juli 2012, 10:20 Uhr
Aufgabe 11.4
Beweisen Sie: Sei 
ein Dreieck mit schulüblichen Bezeichnungen. Es gilt:
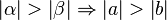
Hinweis: Indirekt (durch Widerspruchsbeweis) in wenigen Schritten machbar!
Lösungsversuch Nummero6/Tchu Tcha Tcha:
Vor.: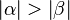 
Beh.: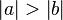 
Annahme 1: 
= 
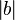
Annahme 2: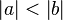 
(1) Wenn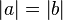 
(Ann.1), dann gilt nach dem BWS: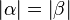 
(2) Widerspruch zur Voraussetzung, Annahme 1 ist zu verwerfen // (1), Vor.
Hat jemand eine Idee, wie ich Annahme 2 begründen kann?!? --Tchu Tcha Tcha 17:30, 6. Jul. 2012 (CEST)
Mit dem Satz IX.2, der bewiesen ist.--Oz44oz 20:26, 6. Jul. 2012 (CEST)
Danke.
(3) 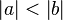(Ann. 2), dann gilt nach dem Satz IX.2 (Der größeren Seite liegt der größere Winkel gegenüber):
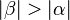
(4) Widerspruch zur Voraussetzung, Annahme 2 ist zu verwerfen // (3), Vor.
(5) Behauptung stimmt. // (2),(4)
qed.
--Tchu Tcha Tcha 13:37, 9. Jul. 2012 (CEST)
- Sieht gut aus und ist kurz und knapp :) --Tutor Andreas 11:20, 10. Jul. 2012 (CEST)
