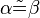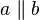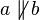Umkehrung des Stufenwinkelsatzes (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> | ||
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
| + | <!--- ------------------------------------------------------------------------------------------ ---> | ||
| + | |||
| + | |||
== Stufenwinkel, Wechselwinkel, entgegengesetzt liegende Winkel == | == Stufenwinkel, Wechselwinkel, entgegengesetzt liegende Winkel == | ||
| Zeile 42: | Zeile 49: | ||
Den Rest können Sie selbst! | Den Rest können Sie selbst! | ||
| + | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
| + | |} | ||
| + | </div> | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 10. Juli 2012, 12:32 Uhr
|
Stufenwinkel, Wechselwinkel, entgegengesetzt liegende WinkelIn welchen Fällen handelt es sich um....
Definition X.1: (Stufenwinkel)Zwei Winkel <(p,q) und <(r,s) heißen Stufenwinkel,... (ergänzen Sie) Definition X.2: (Wechselwinkel)Zwei Winkel <(p, q) und <(r, s) heißen Wechselwinkel,...(ergänzen Sie) Definition X.3: (entgegengesetzt liegende Winkel)Zwei Winkel
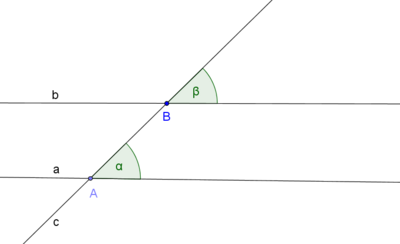
Die Umkehrung des StufenwinkelsatzesSatz X.1: (Umkehrung des Stufenwinkelsatzes)
Beweis von Satz X.1: (Umkehrung des Stufenwinkelsatzes)Es seien Voraussetzung: (i) Behauptung:
Annahme:
Den Rest können Sie selbst! |
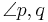 und
und 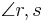 sind entgegengesetzt liegende Winkel,...(ergänzen Sie)
sind entgegengesetzt liegende Winkel,...(ergänzen Sie)
 und
und  zwei nicht identische Geraden, die durch eine dritte Gerade
zwei nicht identische Geraden, die durch eine dritte Gerade  jeweils geschnitten werden. Es seien ferner
jeweils geschnitten werden. Es seien ferner  und
und  zwei Stufenwinkel, die bei dem Schnitt von
zwei Stufenwinkel, die bei dem Schnitt von 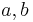 und
und  und die Gerade
und die Gerade  schneiden.
schneiden.