Lösung von Aufg. 12.7 S: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „ Beweisen Sie den Innenwinkelsatz für Dreiecke<br /> '''a)''' mithilfe des Stufenwinkelsatzes.<br /> '''b)''' mithilfe der Umkehrung des Stufenwinkelsatzes.<br /…“) |
|||
| Zeile 1: | Zeile 1: | ||
| − | |||
Beweisen Sie den Innenwinkelsatz für Dreiecke<br /> | Beweisen Sie den Innenwinkelsatz für Dreiecke<br /> | ||
'''a)''' mithilfe des Stufenwinkelsatzes.<br /> | '''a)''' mithilfe des Stufenwinkelsatzes.<br /> | ||
'''b)''' mithilfe der Umkehrung des Stufenwinkelsatzes.<br /> | '''b)''' mithilfe der Umkehrung des Stufenwinkelsatzes.<br /> | ||
| + | |||
| + | '''a) Lösungsversuch Nummero6/Tchu Tcha Tcha:'''<br /> | ||
| + | Vor.: Dreieck <math>\overline{ABC}</math> mit schulüblichen Bezeichnungen<br /> | ||
| + | Beh.: <math>\left|\alpha \right| + \left|\beta \right| +\left|\gamma \right| = 180</math><br /> | ||
| + | Ann.:<math>\left|\alpha \right| + \left|\beta \right| +\left|\gamma \right| \neq 180</math><br /> | ||
| + | |||
| + | Skizze folgt.. | ||
| + | |||
| + | (1) <math>\exists g: g\|| AB \wedge C\in g</math> // Vor., EPA<br /> | ||
| + | (2) <math>\alpha \tilde {=} \alpha'</math> // (1), Def. Stufenwinkel, Stufenwinkelsatz<br /> | ||
| + | (3) <math>\beta \tilde {=} \beta'</math> // (1), Def. Wechselwinkel, Wechselwinkelsatz<br /> | ||
| + | (4) <math>\gamma \tilde {=} \gamma'</math> // (1), Def. Scheitelwinkel, Scheitelwinkelsatz<br /> | ||
| + | (5) <math>\left|\alpha' \right| + \left|\beta' \right| +\left|\gamma' \right| = 180</math> // (2-4), Def.gestreckter Winkel(??)<br /> | ||
| + | (6) <math>\left|\alpha \right| + \left|\beta \right| +\left|\gamma \right| = 180</math>//(2-4)<br /> | ||
| + | (7) Widerspruch zur Annahme // (6)<br /> | ||
| + | (8) Behauptung stimmt // (7)<br /> | ||
| + | qed<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 17:33, 13. Jul. 2012 (CEST) | ||
| + | |||
| + | |||
<br /> | <br /> | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Version vom 13. Juli 2012, 16:33 Uhr
Beweisen Sie den Innenwinkelsatz für Dreiecke
a) mithilfe des Stufenwinkelsatzes.
b) mithilfe der Umkehrung des Stufenwinkelsatzes.
a) Lösungsversuch Nummero6/Tchu Tcha Tcha:
Vor.: Dreieck 
mit schulüblichen Bezeichnungen
Beh.: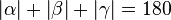 
Ann.: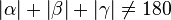
Skizze folgt..
(1) 
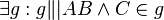// Vor., EPA
(2) 
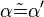// (1), Def. Stufenwinkel, Stufenwinkelsatz
(3) 
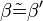// (1), Def. Wechselwinkel, Wechselwinkelsatz
(4) 
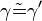// (1), Def. Scheitelwinkel, Scheitelwinkelsatz
(5) 
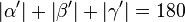// (2-4), Def.gestreckter Winkel(??)
(6) 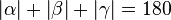//(2-4)
(7) Widerspruch zur Annahme // (6)
(8) Behauptung stimmt // (7)
qed
--Tchu Tcha Tcha 17:33, 13. Jul. 2012 (CEST)
