Spickzettel SS 12 Sekundarstufe: Unterschied zwischen den Versionen
| Zeile 51: | Zeile 51: | ||
| − | |||
| − | |||
| − | |||
| − | |||
'''Existenz kann nicht mit Definitionen begründet werden''' | '''Existenz kann nicht mit Definitionen begründet werden''' | ||
| Zeile 117: | Zeile 113: | ||
'''Stufenwinkelsatz:''' | '''Stufenwinkelsatz:''' | ||
l α l ≅ l β l => a ll b | l α l ≅ l β l => a ll b | ||
| − | + | ||
| − | + | ||
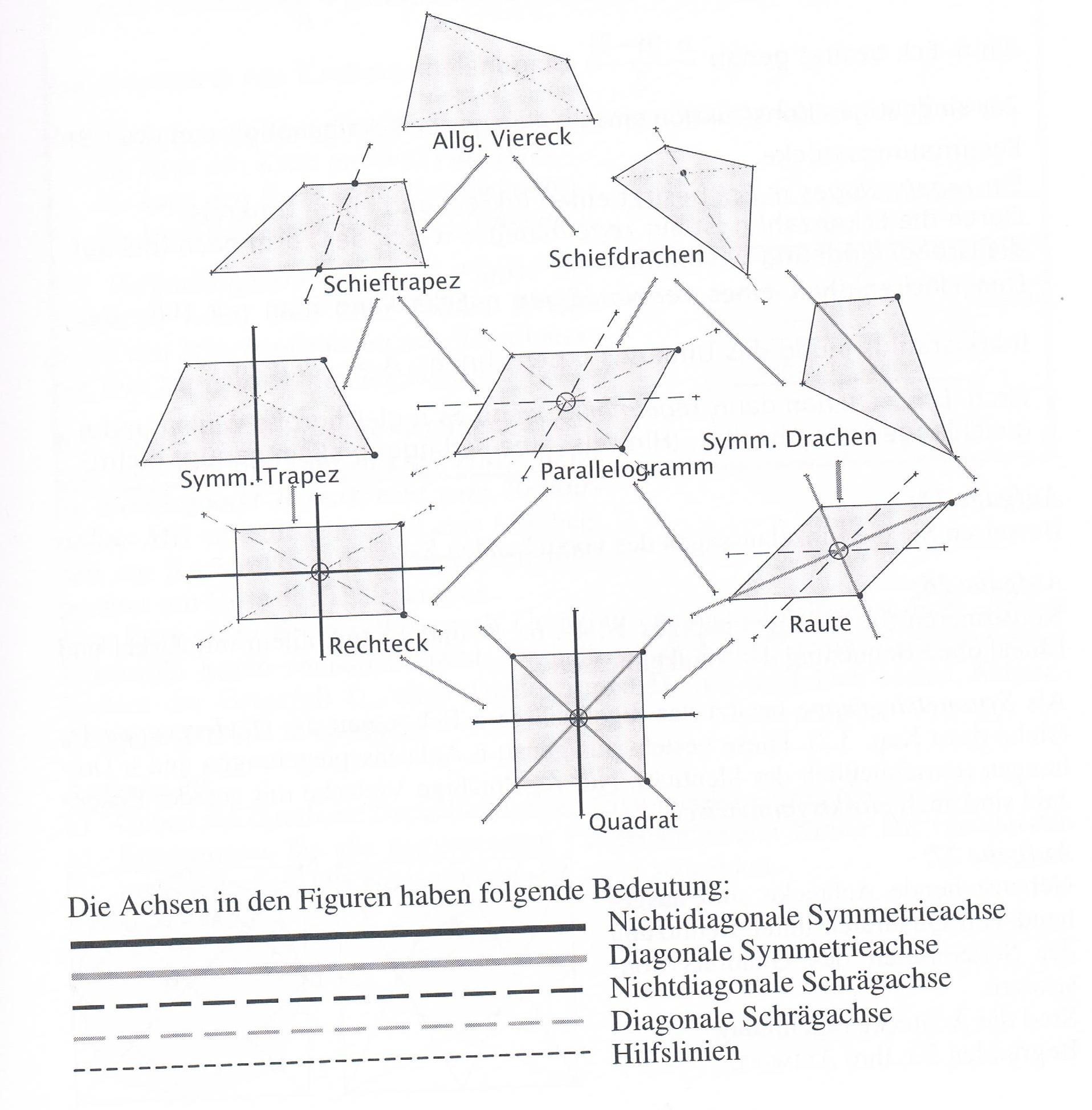
'''Haus der Vierecke:''' | '''Haus der Vierecke:''' | ||
Version vom 22. Juli 2012, 14:54 Uhr
Wie gesagt, eine A4-Seite, nutzen Sie für den Disput untereinander ausnahmsweise die Diskussionsseite dieser Datei.
Ich hab die bisherigen Kommentare mal ausnahmsweise in die Diskussionsseite gelegt. Also hier meine Vorschläge für Sätze:
- Existenz und Eindeutigkeit des Mittelpunktes einer Strecke
- Existenz und Eindeutigkeit der Mittelsenkrechten einer Strecke
- Existenz und Eindeutigkeit der Senkrechten durch einen Punkt
 bzgl. einer Geraden
bzgl. einer Geraden 
- Existenz und Eindeutigkeit des Lotes
- Existenz und Eindeutigkeit der Winkelhalbierenden
...--*m.g.* 15:49, 10. Jul. 2012 (CEST)
Spickzettel
Satz: Jede Strecke hat genau einen Mittelpunkt ∃M := IPMI = IMQI M ∈ P¯G
A <=> B
A ist äquivalent zu B
A ist notwendig und hinreichend für B
A => B A ist eine hinreichende Bedingung für B B ist eine notwendige Bedingung für A
Definition Inneres eines Winkels: I< ASB := SA,B+ ∩ SB,A+
Winkelhalbierenden Kriterium: < ASB P ∊ w <=> lP,SA+l = lP,SB+l
Basiswinkelsatz:
a ≅ b => α ≅ β
S s W – Satz: Größere Seite => größerem Winkel gegenüber
dieser muss gezeigt werden
Außenwinkelsatz: Außenwinkel β´ => β´> α β´> γ
Kriterium: Sei ABC ein
Dreieck mit schulüb. Bez.:
I a l > l b l <=> l α l > l β l
Existenz kann nicht mit Definitionen begründet werden
Definition Strecke (AB):
A¯B :={ P l Zw(A,P,B) } ∪ {A,B}
Mittelsenkrechten Kriterium:
P ∊ m <=> lAPl = lBPl
Definition Halbgerade: offene Halbebene: A,B ∊ g; A≠B
AB+ := { P l Zw(A,P,B) v Zw(A,B,P) } ∪ {B}
AB- := { P l Zw(P,A,B) }
geschloss. Halbebene: A,B ∊ g; A≠B
AB+ := { P l Zw(A,P,B) v Zw(A,B,P) } ∪ {A,B}
AB- := { P l Zw(P,A,B) }∪ {A}
Definition Halbebene:
offene Halbebene: Q∉g
gQ+ := { P l P¯Q ∩ g = ∅ } ∪ {A,B}
gQ- := { P l P¯Q ∩g ≠ ∅ }
geschloss. Halbebene: Q∉g
gQ+ := { P l P¯Q ∩ g = ∅ } ∪ g
gQ- := { P l P¯Q ∩ g ≠ ∅ } ∪ g
Beweis: Zw(A,B,C) => A¯B ⊂ A¯C
a) A¯B ist Teilmenge von A¯C
b) A¯B ≠ A¯C
das bedeutet ∀P∊ A¯B : P∊ A¯C bzw. wenn P∊ A¯B => P∊ A¯C
Stufenwinkelsatz:
l α l ≅ l β l => a ll b
Haus der Vierecke:
--KeinKurpfälzer 14:25, 22. Jul. 2012 (CEST) H2O und Co