Spickzettel SS 12 Sekundarstufe
Datei:Dok1.doc habs mal alles auf einem dinA4 blatt zusammengestellt... ob es soviel hilft? schaden kann es sicher nicht(hoffe ich). Im übrigen ohne gewähr. habs aufgrund der späten zeit so übernommen wie es hier steht--LuLu7410 01:00, 23. Jul. 2012 (CEST)
Beitrag M.G.
- Existenz und Eindeutigkeit des Mittelpunktes einer Strecke
- Existenz und Eindeutigkeit der Mittelsenkrechten einer Strecke
- Existenz und Eindeutigkeit der Senkrechten durch einen Punkt
 bzgl. einer Geraden
bzgl. einer Geraden 
- Existenz und Eindeutigkeit des Lotes
- Existenz und Eindeutigkeit der Winkelhalbierenden
und ganz wichtig:
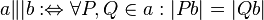 --*m.g.* 20:11, 22. Jul. 2012 (CEST)
--*m.g.* 20:11, 22. Jul. 2012 (CEST)
Beitrag Studierende
Und natürlich die oben genannten Sätze von M.G.!!!!!!!!!!!!!!!!!!!!
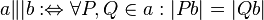
Satz: Jede Strecke hat genau einen Mittelpunkt
∃M := IPMI = IMQI M ∈ P¯G
A <=> B
A ist äquivalent zu B
A ist notwendig und hinreichend für B
A => B
A ist eine hinreichende Bedingung für B
B ist eine notwendige Bedingung für A
Definition Inneres eines Winkels:
I< ASB := SA,B+ ∩ SB,A+
Winkelhalbierenden Kriterium:
< ASB
P ∊ w <=> lP,SA+l = lP,SB+l
S s W – Satz: Größere Seite => größerem Winkel gegenüber (dieser muss gezeigt werden)
Außenwinkelsatz:
Außenwinkel β´ => β´> α
β´> γ
Kriterium: Sei ABC ein
Dreieck mit schulüb. Bez.:
I a l > l b l <=> l α l > l β l
Existenz kann nicht mit Definitionen begründet werden
Definition Strecke (AB):
A¯B :={ P l Zw(A,P,B) } ∪ {A,B}
Mittelsenkrechten Kriterium:
P ∊ m <=> lAPl = lBPl
Definition Halbgerade:
offene Halbgerade: A,B ∊ g; A≠B
AB+ := { P l Zw(A,P,B) v Zw(A,B,P) } ∪ {B}
AB- := { P l Zw(P,A,B) }
geschloss. Halbgerade: A,B ∊ g; A≠B
AB+ := { P l Zw(A,P,B) v Zw(A,B,P) } ∪ {A,B}
AB- := { P l Zw(P,A,B) }∪ {A}
Definition Halbebene:
offene Halbebene: Q∉g
gQ+ := { P l P¯Q ∩ g = ∅ } ∪ {A,B}
Warum vereinigt mit A und B? Was ist denn A und B?--Tutorin Anne 12:03, 23. Jul. 2012 (CEST)
gQ- := { P l P¯Q ∩g ≠ ∅ }
geschloss. Halbebene: Q∉g
gQ+ := { P l P¯Q ∩ g = ∅ } ∪ g
gQ- := { P l P¯Q ∩ g ≠ ∅ } ∪ g
Beweis: Zw(A,B,C) => A¯B ⊂ A¯C
a) A¯B ist Teilmenge von A¯C
b) A¯B ≠ A¯C
das bedeutet ∀P∊ A¯B : P∊ A¯C
bzw. wenn P∊ A¯B => P∊ A¯C
Ist das die Beweisidee? Ich weiß nicht genau, was die letzten Zeilen hier aussagen sollen.--Tutorin Anne 12:03, 23. Jul. 2012 (CEST)
Stufenwinkelsatz:
l α l ≅ l β l => a ll b
Das ist die Umkehrung des Stufenwinkelsatzes, nicht der Stufenwinkelsatz.--Tutorin Anne 12:03, 23. Jul. 2012 (CEST)