Lösung von Aufgabe 4.2 P (WS 12 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „a) Definieren Sie die Begriffe: "gleichseitiges Dreieck" und "gleichschenkliges Dreieck". Die Begriffe "Dreieck" und "Seite eines Dreiecks" seien bereits definier…“)
 
Zeile 1: Zeile 1:
 
a) Definieren Sie die Begriffe: "gleichseitiges Dreieck" und "gleichschenkliges Dreieck". Die Begriffe "Dreieck" und "Seite eines Dreiecks" seien bereits definiert. <br />
 
a) Definieren Sie die Begriffe: "gleichseitiges Dreieck" und "gleichschenkliges Dreieck". Die Begriffe "Dreieck" und "Seite eines Dreiecks" seien bereits definiert. <br />
 +
 +
Ein gleichseitiges Dreieck ist ein Dreieck, bei dem alle Seiten gleich lang sind.--[[Benutzer:Der Bohrer|Der Bohrer]] 11:45, 22. Nov. 2012 (CET)
 +
 +
Ein gleichschenkliges Dreieck ist ein Dreieck mit zwei gleich langen Seiten.--[[Benutzer:Der Bohrer|Der Bohrer]] 11:45, 22. Nov. 2012 (CET)
 +
 
b) Beweisen Sie durch Kontraposition: Jedes gleichseitige Dreieck ist auch ein gleichschenkliges Dreieck.<br />
 
b) Beweisen Sie durch Kontraposition: Jedes gleichseitige Dreieck ist auch ein gleichschenkliges Dreieck.<br />
  
 +
<math>\left( A\Rightarrow B\right) \Leftrightarrow  \left(\neg B\Rightarrow \neg A\right)  </math>
 +
Wenn ein Dreieck also nicht gleichschenklig ist <math>\left(\neg B\right)</math> , dann ist es auch nicht gleichseitig <math>\left( \neg A \right)</math> .
 +
Da diese Implikation stimmt, stimmt auch die Äquivalenz.--[[Benutzer:Der Bohrer|Der Bohrer]] 11:45, 22. Nov. 2012 (CET)
  
  

Version vom 22. November 2012, 11:45 Uhr

a) Definieren Sie die Begriffe: "gleichseitiges Dreieck" und "gleichschenkliges Dreieck". Die Begriffe "Dreieck" und "Seite eines Dreiecks" seien bereits definiert.

Ein gleichseitiges Dreieck ist ein Dreieck, bei dem alle Seiten gleich lang sind.--Der Bohrer 11:45, 22. Nov. 2012 (CET)

Ein gleichschenkliges Dreieck ist ein Dreieck mit zwei gleich langen Seiten.--Der Bohrer 11:45, 22. Nov. 2012 (CET)

b) Beweisen Sie durch Kontraposition: Jedes gleichseitige Dreieck ist auch ein gleichschenkliges Dreieck.

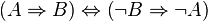\left( A\Rightarrow B\right) \Leftrightarrow \left(\neg B\Rightarrow \neg A\right) Wenn ein Dreieck also nicht gleichschenklig ist 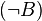\left(\neg B\right) , dann ist es auch nicht gleichseitig 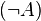\left( \neg A \right) . Da diese Implikation stimmt, stimmt auch die Äquivalenz.--Der Bohrer 11:45, 22. Nov. 2012 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_4.2_P_(WS_12_13)&oldid=18901“