Lösung von Aufgabe 7.2 WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Lösung von User Hazel12) |
(→Lösung von User Hazel12) |
||
| Zeile 28: | Zeile 28: | ||
Die Menge aller Punkte P einer Ebene, die von einem festen Punkt M den selben Abstand r haben, bilden einen Kreis. | Die Menge aller Punkte P einer Ebene, die von einem festen Punkt M den selben Abstand r haben, bilden einen Kreis. | ||
| + | |||
| + | 3: | ||
| + | <u>Sehnen:</u> | ||
| + | Sehnen sind die Strecken von einem Punkt P e k zu einem anderen Punkt Q e k. | ||
| + | |||
| + | <u>Durchmesser:</u> | ||
| + | Durchmesser sind die Strecken von P e k zu Q e k, die durch M, den Mittelpunkt von k gehen. P,M und Q sind kollinear. | ||
| + | |||
| + | <u>Radien:</u> | ||
| + | Radien sind die Strecken von P e k zum Mittelpunkt von k. | ||
==Lösung von User ...== | ==Lösung von User ...== | ||
Version vom 9. Dezember 2012, 11:31 Uhr
|
Aufgabe 7.2Definieren Sie:
BemerkungDer Äquator und alle Längenkreise der Erdkugel sind Beispiele für Großkreise.
Lösung von User Hazel121. Definition Kugel: Die Menge aller Punkte P des Raumes, die von einem festen Punkt M den selben Abstand r haben und die Menge der Punkte M und aller Punkte zwischen P und M bilden eine Kugel.
Die Menge aller Punkte P einer Ebene, die von einem festen Punkt M den selben Abstand r haben, bilden einen Kreis. 3: Sehnen: Sehnen sind die Strecken von einem Punkt P e k zu einem anderen Punkt Q e k. Durchmesser: Durchmesser sind die Strecken von P e k zu Q e k, die durch M, den Mittelpunkt von k gehen. P,M und Q sind kollinear. Radien: Radien sind die Strecken von P e k zum Mittelpunkt von k. Lösung von User ... |
 und dem Radius
und dem Radius 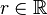 ,
,
 (Durchmesser und Radius sind als geometrische Objekte und nicht als Zahlen zu verstehen),
(Durchmesser und Radius sind als geometrische Objekte und nicht als Zahlen zu verstehen),

