Isomorphie von Gruppen 2012 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
| valign="top" | | | valign="top" | | ||
<!--- hier drüber nichts eintragen ---> | <!--- hier drüber nichts eintragen ---> | ||
| − | {{Definition|(Gruppenisomorphismus)<br />Es seien <math>\left(G, \oplus \right)</math> und <math>\left(H, \otimes \right)</math> zwei Gruppen. Wenn eine Bijektion <math>\varphi</math> von <math>G</math> auf <math>H</math> derart existiert, dass <br /><math>\forall a, b \in G: \varphi(a \oplus b) = \varphi(a) \otimes \varphi(b)</math> gilt, dann sind die beiden Gruppen <math>\left(G, \oplus \right)</math> und <math>\left(H, \otimes \right)</math> | + | {{Definition|(Gruppenisomorphismus)<br />Es seien <math>\left(G, \oplus \right)</math> und <math>\left(H, \otimes \right)</math> zwei Gruppen. Wenn eine Bijektion <math>\varphi</math> von <math>G</math> auf <math>H</math> derart existiert, dass <br /><math>\forall a, b \in G: \varphi(a \oplus b) = \varphi(a) \otimes \varphi(b)</math> gilt, dann sind die beiden Gruppen <math>\left(G, \oplus \right)</math> und <math>\left(H, \otimes \right)</math> isomorph zueinander. Die Abbildung <math>\varphi</math> heißt Gruppenisomorphismus.}} |
Version vom 12. Dezember 2012, 18:32 Uhr
|
Definition (Gruppenisomorphismus) |
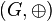 und
und 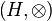 zwei Gruppen. Wenn eine Bijektion
zwei Gruppen. Wenn eine Bijektion  von
von  auf
auf 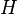 derart existiert, dass
derart existiert, dass 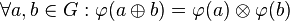 gilt, dann sind die beiden Gruppen
gilt, dann sind die beiden Gruppen 
