Linearkombinationen 2012 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Linearkombinationen) |
*m.g.* (Diskussion | Beiträge) (→Linearkombinationen) |
||
| Zeile 7: | Zeile 7: | ||
<ggb_applet width="773" height="463" version="4.2" ggbBase64="UEsDBBQACAgIAOS+jEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAOS+jEEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5Vrrbts2FP7dPcWBMAzrFse62+7sDknaYQXSrVi6Ydi6H5TI2FxkUZUo28naJ1ufYc+0Q1KyZatO4zRrXSw3iuLhuXzn4yFlZfjtYprAjOUFF+nIcg5tC1gaC8rT8cgq5Xmnb3378LPhmIkxi3IC5yKfEjmy/EPXWs3D3qGv5nI6srxzSoM+Yx3bs4OOH8W9TtT3gg4NbEqpRwJGAwtgUfAHqfiBTFmRkZidxRM2JaciJlKrnEiZPeh25/P5YW38UOTj7ngcHS4KagE6nhYjq7p4gOrWJs09Le7attP99empUd/haSFJGjMLVFAlf/jZveGcp1TMYc6pnIysvo1hTBgfTzDKUHW6SijDUDMWSz5jBU5tdHXMcppZWoykavyeuYJkGY4FlM84ZfnIsg9djF/knKWyGnUqK916/nDG2dwoUlfahm8Peog5L3iUsJF1TpIC4+DpeY4Yogt5id1CXiYsInndX3ngHOA3CvArpnRhYCbwkeUO7APX6R30bPsgCKqIm4YtkEIkWqsNwQBevQLXdm04UI1jGhebMDRDtrlne6ZxTeObJjAyvpnuG1HfyPhGxveuibPqrwKtbqxFWsfpNeN0MD71i1k98O12nP1GnI4K4hU4ynvdeKD8drT/qvGrbmi6Pd04tmmcarCv/mi8wveMyLtVRE7DquHDdqMtvtQWez3v5hbd94pzGaX7tijdYEuU7wlubdQJGkbRlv7Rvy2T3k5xboV2B4uh/z5r/xYGe/aHMDjs1pVuWK09KCZKtqKrZNNCVR1voAsPOBDgwgx7WCcCcAbY9NQCdcEJwA+w6/QhVG0PPLUmffCgD0rO8UCXl6CPf3y9XkMIUJe62TMLFzwfAg8cXZR8wFIEurBhkXM9lAgCCHCSsu4os14Ifogdrw8+OqhKWk+VDQ/nYR+Nu+A54Km5Tg/cEEIXeqosOr6qlmFf+Y5KXQhtCNVUrItYE009xBl98FQ0yPBMFHwJ7oQl2TIrGkeeZqVcwy6e0vpSig1pKuKL4w2sGSlkfY1CuBmtNjmzOa3tgfeGCYlYggeFM0UDgBlJ1ArW+s9FKqGmgGvujXOSTXhcnDEpcVYBf5IZOSWSLb5D6aJ2UJvWW/OQlXHCKSfpL8gRpUIphHqn1nWp3ql9LzBWYiFyenZZIHFg8RvLhS4mh3bzC9G8rIYGbmuoiImifLAxCY1dbhmqAmSzZWhkwYoay3HOafP6SXEsErrMRyZ4Kk9IJstcH7rQTq5iOkrHCdPQ6qqK55f4IhKLM4OpZ3Q9v8ywZxv70fhEJCIHXI9ugEeMcdVGptUyyrGllK1lbC1h10nidDnuDFwtodvItFoKs25cqwJ16igduzbDC11FUHmTY5oy6jRUplye1h3J44sqUsfI/1BOI2RbNW1dpXNHKofdDX4NL1iessSwKMVElqIsDK2X1Lw3LAv2jMjJUUp/YmNcj8+IKokSVRvRlceUxXyKE839Cjqi0vozumruUjbOWR1hoo+5Blg9ajc53bqtVX2Xi+mTdPYcObPh6rBbxzMs4pxnipkQYY2+YCv2UV4QrPC0OQ+DLzCKWFUbBFIqEC0gpZyIXJ9kcc2qZQ2P2BVToGKdxEWuFmzCpniqBalpqZm9TNCP+oCsMgEi+hPLyEYCV7jh8FspqslMkmxC1CG6AiEhl+hAExat76mgm2BhLnREWBoyw4qMMcMn4y9eZKhOr8JGwjX6BSyMUbis2ivzuGSeDlSkamWuFUFzdyNtyDoD0jvgOvr04fIquLw7gisW0ylJKaT6CPILYiJya7X3EVuRDIijwDPIlLIeKI2ySkUL+5lRVoNbvgP8Rrjb0Ldvj/12BFeqlgVY4pZ6gQ+Nhd4lZLUf6IvvOaVMnxc2q0hhKmNMcskKrH9GAB+Nc/lMZQHYIlNg7sDX40+fr26Fdsf54IQ9bhF2thNhZ3tC2BaEe8zYk0+fsfWG5H5wwp60CDvfibDzPSHsJoIfma/rCThFH24KP7kefhXOElyyJ+B33I0D1Q3Rd98OP3uZroHPp1nCYy5vC3K7KEc7gBztCcjOBsM7ewLykQF53gI53gHkeE9AbjE53CuQZy2Q6Q4g0z0BucXkwUcA+UmqHvURhA2kY4N01EL60fVIr59JHt3qTBL2NdSqiUxzB2Avj3JhBbd/p4eLbTgSgyNt4fh4Fxwf7w2O9QHD6f8nMF53RnvUwvBqpzPa1Z6s+/opGB8qgv07pF2XgcetDLCdMsD2JAM1if39SADezdGSenaqgHjOFhKflrT4Fy9LIb/5HF6IGcv1R+kkz8X8rx+PXo9eJGQaUQIvYipkW+L49dcvpuW20ZPX8LlRrh1az5xED6x1dz5m7nhxSp6zXzc/ktbvZQqW8/PlOzwsQE+rvdW8r7GtOi92Kx+KDFjAwrXXH0H1GdXAbz6EXp+wf/6uslW8zOWXV/AVXN2HLujeDHuz++Yl1DrIaTlF32OroUU5iEGWVfiqRNwYU+cGfr5p+snQM7b0c469+c38fLPpp6v+CeQuHVWUc2+wAswYfA1faoL8/s/ff9zHnrm9fVlAa96bd89rLJi3gNRaMe7/bMW416yYbvMljH4jWv0T1MN/AVBLBwiIZIB8ogcAALMlAABQSwECFAAUAAgICADkvoxB1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAOS+jEGIZIB8ogcAALMlAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAOQgAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="773" height="463" version="4.2" ggbBase64="UEsDBBQACAgIAOS+jEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAOS+jEEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5Vrrbts2FP7dPcWBMAzrFse62+7sDknaYQXSrVi6Ydi6H5TI2FxkUZUo28naJ1ufYc+0Q1KyZatO4zRrXSw3iuLhuXzn4yFlZfjtYprAjOUFF+nIcg5tC1gaC8rT8cgq5Xmnb3378LPhmIkxi3IC5yKfEjmy/EPXWs3D3qGv5nI6srxzSoM+Yx3bs4OOH8W9TtT3gg4NbEqpRwJGAwtgUfAHqfiBTFmRkZidxRM2JaciJlKrnEiZPeh25/P5YW38UOTj7ngcHS4KagE6nhYjq7p4gOrWJs09Le7attP99empUd/haSFJGjMLVFAlf/jZveGcp1TMYc6pnIysvo1hTBgfTzDKUHW6SijDUDMWSz5jBU5tdHXMcppZWoykavyeuYJkGY4FlM84ZfnIsg9djF/knKWyGnUqK916/nDG2dwoUlfahm8Peog5L3iUsJF1TpIC4+DpeY4Yogt5id1CXiYsInndX3ngHOA3CvArpnRhYCbwkeUO7APX6R30bPsgCKqIm4YtkEIkWqsNwQBevQLXdm04UI1jGhebMDRDtrlne6ZxTeObJjAyvpnuG1HfyPhGxveuibPqrwKtbqxFWsfpNeN0MD71i1k98O12nP1GnI4K4hU4ynvdeKD8drT/qvGrbmi6Pd04tmmcarCv/mi8wveMyLtVRE7DquHDdqMtvtQWez3v5hbd94pzGaX7tijdYEuU7wlubdQJGkbRlv7Rvy2T3k5xboV2B4uh/z5r/xYGe/aHMDjs1pVuWK09KCZKtqKrZNNCVR1voAsPOBDgwgx7WCcCcAbY9NQCdcEJwA+w6/QhVG0PPLUmffCgD0rO8UCXl6CPf3y9XkMIUJe62TMLFzwfAg8cXZR8wFIEurBhkXM9lAgCCHCSsu4os14Ifogdrw8+OqhKWk+VDQ/nYR+Nu+A54Km5Tg/cEEIXeqosOr6qlmFf+Y5KXQhtCNVUrItYE009xBl98FQ0yPBMFHwJ7oQl2TIrGkeeZqVcwy6e0vpSig1pKuKL4w2sGSlkfY1CuBmtNjmzOa3tgfeGCYlYggeFM0UDgBlJ1ArW+s9FKqGmgGvujXOSTXhcnDEpcVYBf5IZOSWSLb5D6aJ2UJvWW/OQlXHCKSfpL8gRpUIphHqn1nWp3ql9LzBWYiFyenZZIHFg8RvLhS4mh3bzC9G8rIYGbmuoiImifLAxCY1dbhmqAmSzZWhkwYoay3HOafP6SXEsErrMRyZ4Kk9IJstcH7rQTq5iOkrHCdPQ6qqK55f4IhKLM4OpZ3Q9v8ywZxv70fhEJCIHXI9ugEeMcdVGptUyyrGllK1lbC1h10nidDnuDFwtodvItFoKs25cqwJ16igduzbDC11FUHmTY5oy6jRUplye1h3J44sqUsfI/1BOI2RbNW1dpXNHKofdDX4NL1iessSwKMVElqIsDK2X1Lw3LAv2jMjJUUp/YmNcj8+IKokSVRvRlceUxXyKE839Cjqi0vozumruUjbOWR1hoo+5Blg9ajc53bqtVX2Xi+mTdPYcObPh6rBbxzMs4pxnipkQYY2+YCv2UV4QrPC0OQ+DLzCKWFUbBFIqEC0gpZyIXJ9kcc2qZQ2P2BVToGKdxEWuFmzCpniqBalpqZm9TNCP+oCsMgEi+hPLyEYCV7jh8FspqslMkmxC1CG6AiEhl+hAExat76mgm2BhLnREWBoyw4qMMcMn4y9eZKhOr8JGwjX6BSyMUbis2ivzuGSeDlSkamWuFUFzdyNtyDoD0jvgOvr04fIquLw7gisW0ylJKaT6CPILYiJya7X3EVuRDIijwDPIlLIeKI2ySkUL+5lRVoNbvgP8Rrjb0Ldvj/12BFeqlgVY4pZ6gQ+Nhd4lZLUf6IvvOaVMnxc2q0hhKmNMcskKrH9GAB+Nc/lMZQHYIlNg7sDX40+fr26Fdsf54IQ9bhF2thNhZ3tC2BaEe8zYk0+fsfWG5H5wwp60CDvfibDzPSHsJoIfma/rCThFH24KP7kefhXOElyyJ+B33I0D1Q3Rd98OP3uZroHPp1nCYy5vC3K7KEc7gBztCcjOBsM7ewLykQF53gI53gHkeE9AbjE53CuQZy2Q6Q4g0z0BucXkwUcA+UmqHvURhA2kY4N01EL60fVIr59JHt3qTBL2NdSqiUxzB2Avj3JhBbd/p4eLbTgSgyNt4fh4Fxwf7w2O9QHD6f8nMF53RnvUwvBqpzPa1Z6s+/opGB8qgv07pF2XgcetDLCdMsD2JAM1if39SADezdGSenaqgHjOFhKflrT4Fy9LIb/5HF6IGcv1R+kkz8X8rx+PXo9eJGQaUQIvYipkW+L49dcvpuW20ZPX8LlRrh1az5xED6x1dz5m7nhxSp6zXzc/ktbvZQqW8/PlOzwsQE+rvdW8r7GtOi92Kx+KDFjAwrXXH0H1GdXAbz6EXp+wf/6uslW8zOWXV/AVXN2HLujeDHuz++Yl1DrIaTlF32OroUU5iEGWVfiqRNwYU+cGfr5p+snQM7b0c469+c38fLPpp6v+CeQuHVWUc2+wAswYfA1faoL8/s/ff9zHnrm9fVlAa96bd89rLJi3gNRaMe7/bMW416yYbvMljH4jWv0T1MN/AVBLBwiIZIB8ogcAALMlAABQSwECFAAUAAgICADkvoxB1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAOS+jEGIZIB8ogcAALMlAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAOQgAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
=Linearkombinationen= | =Linearkombinationen= | ||
| − | {{Definition|(Linearkombination)<br />Als Linearkombination der Vektoren <math>\vec{v_1}, \vec{v_2}, ... , \vec{v_n}</math> bezeichnet man den Vektor <math>\vec{x}=\lambda_1\cdot \vec{v_1}+ \lambda_2 \cdot \vec{v_2} + ... + \lambda_n \cdot \vec{v_n}= \sum_{i=1}^n \lambda_i \cdot \vec{v_i}</math> (mit <math>\lambda_1, \lambda_2, ... ,\lambda_n \in \mathbb{R}</math>).}} | + | {{Definition|(Linearkombination)<br />Als Linearkombination der Vektoren <math>\vec{v_1}, \vec{v_2}, ... , \vec{v_n}</math> bezeichnet man den Vektor<br /> <math>\vec{x}=\lambda_1\cdot \vec{v_1}+ \lambda_2 \cdot \vec{v_2} + ... + \lambda_n \cdot \vec{v_n}= \sum_{i=1}^n \lambda_i \cdot \vec{v_i}</math> (mit <math>\lambda_1, \lambda_2, ... ,\lambda_n \in \mathbb{R}</math>).}} |
<!--- hier drunter nichts eintragen ---> | <!--- hier drunter nichts eintragen ---> | ||
[[Kategorie:Linalg]] | [[Kategorie:Linalg]] | ||
Version vom 13. Dezember 2012, 00:07 Uhr
Darstellung von Vektoren mittels anderer Vektoren
LinearkombinationenDefinition (Linearkombination) |
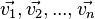bezeichnet man den Vektor
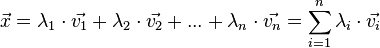(mit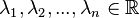 
).
