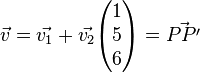Lösungen zu den Aufgaben 4: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎4.3)
(→‎4.2)
Zeile 5: Zeile 5:
 
==4.2==
 
==4.2==
 
a) <math>\vec{PP'}=\vec{v}=\begin{pmatrix} 3 \\ 2 \\ -4 \end{pmatrix}</math><br />
 
a) <math>\vec{PP'}=\vec{v}=\begin{pmatrix} 3 \\ 2 \\ -4 \end{pmatrix}</math><br />
−
b) <math>\vec{A'}=\vec{OA}+\vec{PP'}=\begin{pmatrix} 6 \\ 0 \\ 0 \end{pmatrix}</math><br />
+
b) <math>\vec{OA'}=\vec{OA}+\vec{PP'}=\begin{pmatrix} 6 \\ 0 \\ 0 \end{pmatrix}</math><br />
−
<math>\vec{B'}=\vec{OB}+\vec{PP'}=\begin{pmatrix} 6,5 \\ 4,5 \\ -9 \end{pmatrix}</math><br />
+
<math>\vec{OB'}=\vec{OB}+\vec{PP'}=\begin{pmatrix} 6,5 \\ 4,5 \\ -9 \end{pmatrix}</math><br />
  
 
==4.3==
 
==4.3==

Version vom 27. Dezember 2012, 17:13 Uhr

4.1

a) 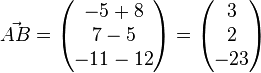\vec{AB}=\begin{pmatrix} -5 +8 \\ 7-5 \\ -11-12 \end{pmatrix}=\begin{pmatrix} 3 \\ 2 \\ -23 \end{pmatrix}
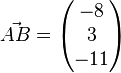
b) \vec{AB}=\begin{pmatrix} -8 \\ 3 \\ -11 \end{pmatrix}

4.2

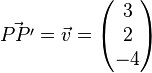
a) \vec{PP'}=\vec{v}=\begin{pmatrix} 3 \\ 2 \\ -4 \end{pmatrix}
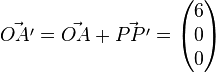
b) \vec{OA'}=\vec{OA}+\vec{PP'}=\begin{pmatrix} 6 \\ 0 \\ 0 \end{pmatrix}
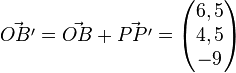
\vec{OB'}=\vec{OB}+\vec{PP'}=\begin{pmatrix} 6,5 \\ 4,5 \\ -9 \end{pmatrix}

4.3

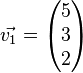
\vec{v_1}=\begin{pmatrix} 5 \\ 3 \\ 2 \end{pmatrix}

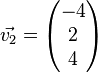
\vec{v_2}=\begin{pmatrix} -4 \\ 2 \\ 4 \end{pmatrix}

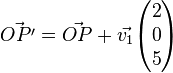
a) \vec{OP'}=\vec{OP}+\vec{v_1}\begin{pmatrix} 2 \\ 0 \\ 5 \end{pmatrix}

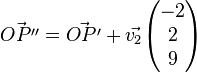
\vec{OP''}=\vec{OP'}+\vec{v_2}\begin{pmatrix} -2 \\ 2 \\ 9 \end{pmatrix}

b) \vec{v}=\vec{v_1}+\vec{v_2}\begin{pmatrix} 1 \\ 5 \\ 6 \end{pmatrix}=\vec{PP'}

Von „http://geometrie.zum.de/index.php?title=Lösungen_zu_den_Aufgaben_4&oldid=19916“