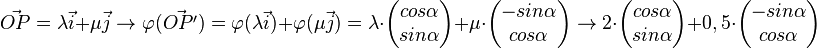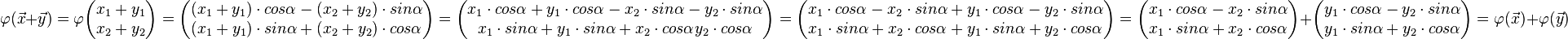Lineare Abbildungen, Vektorraumisomorphismus 2012 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Drehung)
(→‎Drehung)
Zeile 42: Zeile 42:
 
  \begin{pmatrix} x_1 \cdot cos  \alpha -x_2 \cdot sin \alpha \\ x_1 \cdot sin \alpha + x_2 \cdot cos \alpha \end{pmatrix} +  
 
  \begin{pmatrix} x_1 \cdot cos  \alpha -x_2 \cdot sin \alpha \\ x_1 \cdot sin \alpha + x_2 \cdot cos \alpha \end{pmatrix} +  
 
\begin{pmatrix} y_1 \cdot cos  \alpha - y_2 \cdot sin \alpha \\ y_1 \cdot sin \alpha + y_2 \cdot cos \alpha \end{pmatrix} =  
 
\begin{pmatrix} y_1 \cdot cos  \alpha - y_2 \cdot sin \alpha \\ y_1 \cdot sin \alpha + y_2 \cdot cos \alpha \end{pmatrix} =  
−
\varphi ( \vec{x}) + \varphi ( \vec{y})
+
\varphi ( \vec{x}) + \varphi ( \vec{y})</math>
  
 
==Geradenspiegelung==
 
==Geradenspiegelung==

Version vom 8. Januar 2013, 17:17 Uhr

Inhaltsverzeichnis

Definition

Definition

(lineare Abbildung)
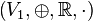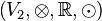Es seien \left(V_1, \oplus, \mathbb{R}, \cdot\right) und \left(V_2, \otimes, \mathbb{R}, \odot\right) zwei Vektorräume über der Körper der reellen Zahlen.
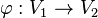Eine Abbildung \varphi: V_1 \rightarrow V_2 heißt lineare Abbildung wenn gilt: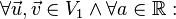
\forall \vec{u}, \vec{v} \in V_1 \wedge \forall a \in \mathbb{R}:
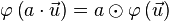
(H) \varphi ist homogen: \varphi\left(a \cdot \vec{u} \right) = a \odot \varphi\left(\vec{u}\right)
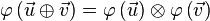
(A) \varphi ist additiv: \varphi\left(\vec{u} \oplus \vec{v} \right)= \varphi \left(\vec{u}\right) \otimes \varphi \left(\vec{v}\right)

Beispiele

senkrechte Parallelprojektion auf die x-y-Ebene

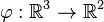
\varphi: \mathbb{R}^3 \rightarrow \mathbb{R}^2
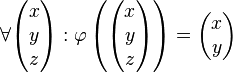
\forall \begin{pmatrix} x \\ y \\ z \end{pmatrix}: \varphi \left( \begin{pmatrix} x \\ y \\ z \end{pmatrix}\right)= \begin{pmatrix} x \\ y \end{pmatrix}
Man beweise: \varphi ist lineare Abbildung

Drehung

Drehungen um den Ursprung des Koordinatensystems

Drehung der kanonischen Basisvektoren
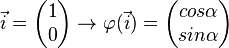
\vec{i} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \rightarrow \varphi( \vec{i}) = \begin{pmatrix} cos \alpha \\ sin \alpha \end{pmatrix}

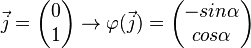
\vec{j} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \rightarrow \varphi( \vec{j}) =\begin{pmatrix} -sin \alpha \\ cos \alpha \end{pmatrix}

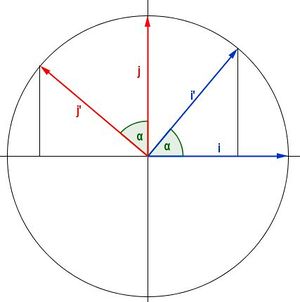
Drehung kanonische Basis.JPG

Drehung anderer Vektoren:
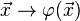
\vec{x} \rightarrow \varphi( \vec{x} )

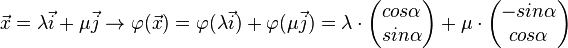
\vec{x} = \lambda \vec{i} + \mu \vec{j} \rightarrow \varphi( \vec{x}) = \varphi ( \lambda \vec{i}) + \varphi( \mu \vec{j}) = \lambda \cdot \begin{pmatrix} cos \alpha \\ sin \alpha \end{pmatrix} + \mu \cdot \begin{pmatrix} -sin \alpha \\ cos \alpha \end{pmatrix}

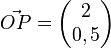Bsp.: \vec{OP} = \begin{pmatrix} 2 \\ 0,5 \end{pmatrix} wird an O um \alpha gedreht.
\vec{OP} = \lambda \vec{i} + \mu \vec{j} \rightarrow \varphi( \vec{OP'}) = \varphi ( \lambda \vec{i}) + \varphi( \mu \vec{j}) = \lambda \cdot \begin{pmatrix} cos \alpha \\ sin \alpha \end{pmatrix} + \mu \cdot \begin{pmatrix} -sin \alpha \\ cos \alpha \end{pmatrix} \rightarrow 2 \cdot \begin{pmatrix} cos \alpha \\ sin \alpha \end{pmatrix} + 0,5 \cdot \begin{pmatrix} -sin \alpha \\ cos \alpha \end{pmatrix}

\vec{OP'} = \begin{pmatrix} cos \alpha & -sin \alpha\\ sin \alpha & cos \alpha \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 0,5 \end{pmatrix} = \begin{pmatrix} 2cos \alpha -0,5sin \alpha\\ 2sin \alpha + 0,5cos \alpha \end{pmatrix}

Drehungsmatrix:
\begin{pmatrix} cos \alpha & -sin \alpha\\ sin \alpha & cos \alpha \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x \cdot cos \alpha -y \cdot sin \alpha\\ x \cdot sin \alpha + y \cdot cos \alpha \end{pmatrix}

Drehung als lineare Abbildung:

Behauptung: \varphi ist eine lineare Abbildung.

Zu zeigen:
(H) \varphi ist homomorph
(A) \varphi ist additiv

Beweis zum Homomorphismus:
\varphi ( \vec{x} + \vec{y}) = \varphi \begin{pmatrix} x_1+y_1 \\ x_2+y_2 \end{pmatrix} = \begin{pmatrix} (x_1+y_1) \cdot cos \alpha -(x_2+y_2) \cdot sin \alpha\\ (x_1+y_1) \cdot sin \alpha + (x_2+y_2) \cdot cos \alpha \end{pmatrix} = \begin{pmatrix} x_1 \cdot cos \alpha + y_1 \cdot cos \alpha -x_2 \cdot sin \alpha - y_2 \cdot sin \alpha\\ x_1 \cdot sin \alpha + y_1 \cdot sin \alpha + x_2 \cdot cos \alpha y_2 \cdot cos \alpha \end{pmatrix} = \begin{pmatrix} x_1 \cdot cos \alpha -x_2 \cdot sin \alpha + y_1 \cdot cos \alpha - y_2 \cdot sin \alpha\\ x_1 \cdot sin \alpha + x_2 \cdot cos \alpha + y_1 \cdot sin \alpha + y_2 \cdot cos \alpha \end{pmatrix} = \begin{pmatrix} x_1 \cdot cos \alpha -x_2 \cdot sin \alpha \\ x_1 \cdot sin \alpha + x_2 \cdot cos \alpha \end{pmatrix} + \begin{pmatrix} y_1 \cdot cos \alpha - y_2 \cdot sin \alpha \\ y_1 \cdot sin \alpha + y_2 \cdot cos \alpha \end{pmatrix} = \varphi ( \vec{x}) + \varphi ( \vec{y})

Geradenspiegelung

Zentrische Streckung

Isomorphe Vektorräume

Definition

Zwei Vektorräume sind isomorph zu einander, wenn sie durch eine bijektive lineare Abbildung aufeinander abgebildet werden können.

Von „http://geometrie.zum.de/index.php?title=Lineare_Abbildungen,_Vektorraumisomorphismus_2012_13&oldid=20054“