Lösung Aufgabe 9.4 WS 12 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Lösung von User Aaliyah)
(→‎Lösung von User ...)
Zeile 11: Zeile 11:
 
Die Winkel <math>\alpha</math> und <math>\beta</math>  heißen Stufenwinkel, wenn entweder ein Schenkel von <math>\alpha</math> Teilmenge des Schenkels von <math>\beta</math> ist oder umgekehrt und die jeweils anderen Schenkel von <math>\alpha und \beta</math> bezüglich t in derselben Ebene liegen.--[[Benutzer:Aaliyah|Aaliyah]] 16:18, 2. Jan. 2013 (CET)
 
Die Winkel <math>\alpha</math> und <math>\beta</math>  heißen Stufenwinkel, wenn entweder ein Schenkel von <math>\alpha</math> Teilmenge des Schenkels von <math>\beta</math> ist oder umgekehrt und die jeweils anderen Schenkel von <math>\alpha und \beta</math> bezüglich t in derselben Ebene liegen.--[[Benutzer:Aaliyah|Aaliyah]] 16:18, 2. Jan. 2013 (CET)
  
−
==Lösung von User ...==
+
==Lösung von User Sweetnightmare5==
  
 +
Es seien g und h zwei voneinander verschiedene, parallele Geraden, die von einer dritten Gerade t in den Punkten A <math>\in</math>  g und B <math>\in</math>  h geschnitten werden. Ferner sei <math>\alpha</math>  ein Winkel mit dem Scheitelpunkt A und <math>\beta</math>  ein Winkel mit dem Scheitelpunkt B.
 +
Die Winkel <math>\alpha</math>  und <math>\beta</math>  heißen Stufenwinkel, wenn der Winkel <math>\beta</math>  Teilmenge des Winkels  <math>\alpha</math>  ist oder umgekehrt und der Schenkel vom Winkel <math>\beta</math>  Teilmenge des Schenkels vom Winkel <math>\alpha</math> , oder umgekehrt ist. --[[Benutzer:Sweetnightmare5|Sweetnightmare5]] 14:01, 10. Jan. 2013 (CET)
  
 
<!--- Was hier drunter steht muss stehen bleiben --->
 
<!--- Was hier drunter steht muss stehen bleiben --->

Version vom 10. Januar 2013, 14:01 Uhr

Aufgabe 9.4

Definieren Sie den Begriff Stufenwinkel.

Lösung von User Aaliyah

Es seien g und h zwei voneinander verschiedene Geraden, die von einer dritten Gerade t in den Punkten A \epsilon g und B \epsilon h geschnitten werden. Ferner sei \alpha ein Winkel mit dem Scheitelpunkt A und \beta ein Winkel mit dem Scheitelpunkt B.
Die Winkel \alpha und \beta heißen Stufenwinkel, wenn entweder ein Schenkel von \alpha Teilmenge des Schenkels von \beta ist oder umgekehrt und die jeweils anderen Schenkel von \alpha und \beta bezüglich t in derselben Ebene liegen.--Aaliyah 16:18, 2. Jan. 2013 (CET)

Lösung von User Sweetnightmare5

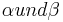Es seien g und h zwei voneinander verschiedene, parallele Geraden, die von einer dritten Gerade t in den Punkten A \in g und B \in h geschnitten werden. Ferner sei \alpha ein Winkel mit dem Scheitelpunkt A und \beta ein Winkel mit dem Scheitelpunkt B. Die Winkel \alpha und \beta heißen Stufenwinkel, wenn der Winkel \beta Teilmenge des Winkels \alpha ist oder umgekehrt und der Schenkel vom Winkel \beta Teilmenge des Schenkels vom Winkel \alpha , oder umgekehrt ist. --Sweetnightmare5 14:01, 10. Jan. 2013 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_Aufgabe_9.4_WS_12_13&oldid=20091“